Difference cochain and chain
A difference cochain is an obstruction to the extension of a homotopy between mappings. Let  be some cellular space, let
be some cellular space, let  be a simply-connected topological space and suppose, moreover, that one is given two mappings
be a simply-connected topological space and suppose, moreover, that one is given two mappings  and a homotopy
and a homotopy
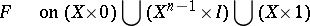 |
(where  and
and  is the
is the  -dimensional skeleton of
-dimensional skeleton of  ) between these mappings on the
) between these mappings on the  -dimensional skeleton. For every oriented
-dimensional skeleton. For every oriented  -dimensional cell
-dimensional cell 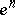 of
of 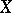 , the restriction of
, the restriction of 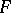 to
to 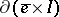 gives a mapping
gives a mapping 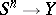 (
(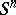 is the
is the  -dimensional sphere) and hence an element of the group
-dimensional sphere) and hence an element of the group 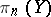 . Thus there arises the cochain
. Thus there arises the cochain 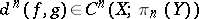 (the notation
(the notation 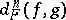 would be more precise), which is called the difference cochain; the cochain
would be more precise), which is called the difference cochain; the cochain 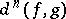 is an obstruction to the extension of
is an obstruction to the extension of 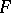 to
to
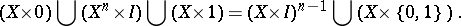 |
The following statements hold: 1) 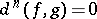 if and only if the homotopy between
if and only if the homotopy between 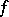 and
and 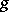 can be extended to
can be extended to 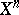 ; 2) the cochain
; 2) the cochain
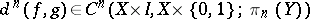 |
is a cocycle; 3) the cohomology class
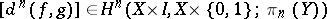 |
vanishes if and only if there is a homotopy between 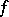 and
and 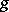 on
on 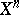 that coincides with
that coincides with 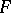 on
on 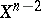 . Without loss of generality one can assume that
. Without loss of generality one can assume that 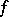 and
and 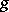 coincide on
coincide on 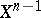 and that
and that 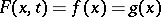 for
for 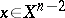 . Then the following statements hold:
. Then the following statements hold:
1) 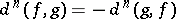 , in particular
, in particular 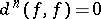 ;
;
2) 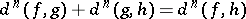 ;
;
3) for any mapping  and for any cochain
and for any cochain 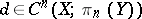 there is a mapping
there is a mapping 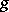 for which
for which 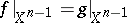 and
and 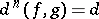 .
.
Now suppose one is given two mappings 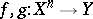 ,
, 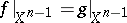 and let
and let 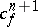 and
and 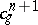 be the obstructions to the extensions of the corresponding mappings. The role of the difference cochain in the theory of obstructions is explained by the following proposition:
be the obstructions to the extensions of the corresponding mappings. The role of the difference cochain in the theory of obstructions is explained by the following proposition:
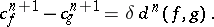 |
Thus, if 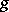 can be extended to
can be extended to 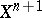 , then
, then 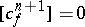 and if
and if 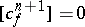 , then
, then 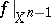 can be extended to
can be extended to 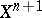 .
.
Comments
References
| [a1] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 228 |
Difference cochain and chain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Difference_cochain_and_chain&oldid=15769