Difference-element-in-K-theory
An element of the group 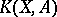 (where
(where 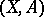 is a pair of spaces and
is a pair of spaces and 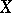 is usually supposed to be a finite cellular space, while
is usually supposed to be a finite cellular space, while  is a cellular subspace of it), constructed from a triple
is a cellular subspace of it), constructed from a triple  , where
, where 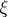 and
and 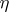 are vector bundles of the same dimension over
are vector bundles of the same dimension over 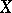 and
and 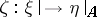 is an isomorphism of vector bundles (here
is an isomorphism of vector bundles (here 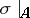 is the part of the vector bundle
is the part of the vector bundle 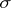 over
over 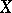 located above the subspace
located above the subspace 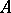 ). The construction of a difference element can be carried out in the following way. First one supposes that
). The construction of a difference element can be carried out in the following way. First one supposes that 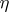 is the trivial bundle and that some trivialization of
is the trivial bundle and that some trivialization of  over
over 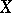 is fixed. Then
is fixed. Then 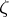 gives a trivialization of
gives a trivialization of  and hence gives an element of the group
and hence gives an element of the group 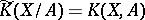 . This element is independent of the choice of the trivialization of
. This element is independent of the choice of the trivialization of 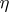 above all of
above all of  . In the general case one chooses a bundle
. In the general case one chooses a bundle  over
over  such that the bundle
such that the bundle  is trivial, and the triple
is trivial, and the triple 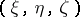 is assigned the same element as the triple
is assigned the same element as the triple 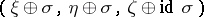 .
.
Comments
References
| [a1] | M.F. Atiyah, F. Hirzebruch, "Analytic cycles on complex manifolds" Topology , 1 (1961) pp. 28–45 |
| [a2] | M.F. Atiyah, R. Bott, A. Shapiro, "Clifford modules" Topology , 3. Suppl. 1 (1964) pp. 3–38 |
Difference-element-in-K-theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Difference-element-in-K-theory&oldid=12228