Dickson polynomial
The Dickson polynomial of the first kind of degree  with parameter
with parameter  is defined by
is defined by
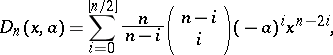 |
where 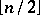 denotes the largest integer
denotes the largest integer 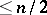 .
.
They satisfy the following recurrence:
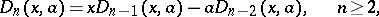 |
where the two initial polynomials are 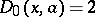 and
and 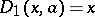 . A second closed form is given by
. A second closed form is given by
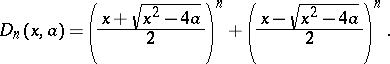 |
There is a functional equation, so that if  can be written as
can be written as 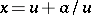 for some
for some  , then
, then
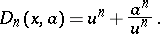 |
The generating function is:
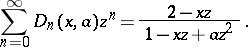 |
Dickson polynomials satisfy a second-order differential equation which corresponds to the well-known differential equation for the classical Chebyshev polynomials. In particular, the polynomial 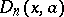 satisfies
satisfies
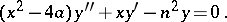 |
Dickson polynomials 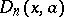 are not unrelated to a well-studied class of polynomials. Consider the classical Chebyshev polynomials
are not unrelated to a well-studied class of polynomials. Consider the classical Chebyshev polynomials 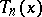 , defined for each integer
, defined for each integer 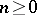 by
by 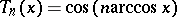 . Over the complex numbers, if
. Over the complex numbers, if 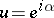 so that
so that 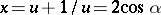 ,
,
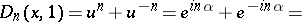 |
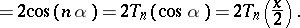 |
Hence Dickson polynomials are related to the classical Chebyshev polynomials, and in fact some authors use the latter terminology.
L.E. Dickson was the first to seriously study various algebraic and number-theoretic properties of these polynomials. In particular, he studied these polynomials as part of his Ph.D. thesis at the University of Chicago in 1896; see also [a4]. In 1923, I. Schur [a16] suggested that these polynomials be named in honour of Dickson.
Properties and applications.
Dickson polynomials have various properties and applications in a variety of areas. Rather than trying to provide too many details here, only a few of these properties and applications are given below; see the various references for additional details. See [a10] for a survey of algebraic and number-theoretic properties as well as applications of Dickson polynomials; see also [a9] for a brief discussion of some of these properties.
Dickson polynomials play a fundamental role in the theory of permutation polynomials over finite fields. For 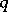 a prime power, let
a prime power, let 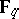 denote the finite field containing
denote the finite field containing 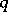 elements. A polynomial with coefficients in
elements. A polynomial with coefficients in 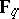 is a permutation polynomial if it induces a one-to-one mapping on the field
is a permutation polynomial if it induces a one-to-one mapping on the field 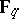 . It is known from [a11], p. 356, that for
. It is known from [a11], p. 356, that for 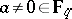 , the Dickson polynomial
, the Dickson polynomial 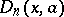 is a permutation polynomial on
is a permutation polynomial on 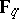 if and only if the greatest common divisor of
if and only if the greatest common divisor of  and
and 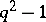 equals
equals 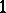 :
:
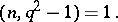 |
(When 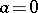 ,
, 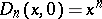 induces a permutation on
induces a permutation on 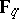 if and only
if and only 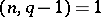 .) S.D. Cohen [a3] has shown that if
.) S.D. Cohen [a3] has shown that if 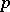 is a large prime number compared to the degree of a polynomial, then the permutation polynomial
is a large prime number compared to the degree of a polynomial, then the permutation polynomial 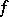 essentially comes from a Dickson polynomial. See [a14] for a discussion of Dickson's work related to permutations (which Dickson called substitution quantics) and his work related to linear groups.
essentially comes from a Dickson polynomial. See [a14] for a discussion of Dickson's work related to permutations (which Dickson called substitution quantics) and his work related to linear groups.
The real importance of Dickson polynomials in the theory of permutations comes from the Schur conjecture. If 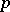 is an odd prime number, reduce an integral polynomial
is an odd prime number, reduce an integral polynomial 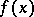 modulo
modulo 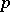 , i.e. reduce the integer coefficients modulo the prime number
, i.e. reduce the integer coefficients modulo the prime number 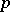 , so that one may view
, so that one may view 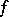 as a function
as a function 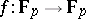 , where
, where 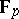 denotes the field of integers modulo
denotes the field of integers modulo 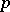 . Using the Dirichlet theorem on prime numbers in an arithmetic progression, it is easy to see that the polynomial
. Using the Dirichlet theorem on prime numbers in an arithmetic progression, it is easy to see that the polynomial 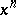 permutes the field
permutes the field 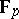 for infinitely many prime numbers
for infinitely many prime numbers 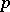 if and only if
if and only if 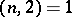 . Similarly, for a non-zero integer
. Similarly, for a non-zero integer  , the Dickson polynomial
, the Dickson polynomial 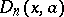 permutes the field
permutes the field 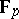 for infinitely many prime numbers
for infinitely many prime numbers 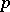 if and only if
if and only if 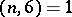 , see [a10], p. 75. In 1923, I. Schur conjectured in [a16] that there are no other integral polynomials that permute the field
, see [a10], p. 75. In 1923, I. Schur conjectured in [a16] that there are no other integral polynomials that permute the field 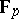 for infinitely many prime numbers
for infinitely many prime numbers 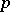 other than compositions of power polynomials
other than compositions of power polynomials 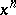 , Dickson polynomials
, Dickson polynomials 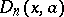 , and linear polynomials
, and linear polynomials 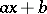 (here,
(here,  and
and 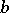 may be rational numbers). The first proof of this conjecture was given by M. Fried [a5]. More recently, in [a17] G. Turnwald proved this using only elementary (i.e., without complex analysis) arguments but the proof is still not easy. No truly easy proof is known (1998). In [a13] G.L. Mullen proved a matrix analogue of Schur's conjecture.
may be rational numbers). The first proof of this conjecture was given by M. Fried [a5]. More recently, in [a17] G. Turnwald proved this using only elementary (i.e., without complex analysis) arguments but the proof is still not easy. No truly easy proof is known (1998). In [a13] G.L. Mullen proved a matrix analogue of Schur's conjecture.
Given a polynomial 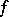 over
over 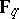 , define the value set
, define the value set 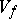 of
of 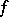 by
by 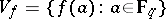 . Since a polynomial of degree
. Since a polynomial of degree  over a field can have at most
over a field can have at most  roots, one has
roots, one has
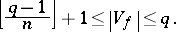 |
Polynomials which achieve the above lower bound are called minimal value-set polynomials, see [a12]. As noted in [a7], polynomials of degree  with value sets of small cardinality (less than twice the minimum) come from Dickson polynomials. As indicated in [a2], Dickson polynomials provide one of the few classes of polynomials over finite fields whose value sets have been determined.
with value sets of small cardinality (less than twice the minimum) come from Dickson polynomials. As indicated in [a2], Dickson polynomials provide one of the few classes of polynomials over finite fields whose value sets have been determined.
If the polynomials (one of each degree) of a class, called a permutable chain of polynomials, over an integral domain commute under composition, then this class must essentially come from the two classes 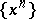 and
and 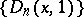 , see [a10], p. 13. Dickson polynomials provide a class of polynomials, one of each degree
, see [a10], p. 13. Dickson polynomials provide a class of polynomials, one of each degree 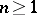 , which can be solved by radicals; see [a18].
, which can be solved by radicals; see [a18].
The construction of irreducible polynomials over finite fields (cf. also Irreducible polynomial) is an important problem and in [a6] it is shown how Dickson polynomials can be effectively used in this regard. For computational work involving finite fields it is useful to have various kinds of bases for extension fields. In this regard, Dickson polynomials again play important roles; see [a6] for polynomial bases and [a1] and [a15] for completely normal bases. Connections between optimal normal bases and Dickson polynomials are discussed in [a10], Sect. 7.5.
Various applications of Dickson polynomials are discussed in [a10], Chap. 7. These applications include cryptology for the secure transmission of information, pseudo-primality testing (cf. also Pseudo-prime; Probabilistic primality test), complete mappings useful in the construction of sets of mutually orthogonal Latin squares (cf. also Latin square), and character sums related to Dickson polynomials (cf. also Weyl sum).
A combinatorial application of Dickson polynomials is developed in [a8], where a study is made of Dickson–Stirling numbers. These generalize the well-studied Stirling numbers of the first and second kinds (cf. Combinatorial analysis). See [a10], Sect. 7.7, for a construction of complete sets of mutually orthogonal Latin squares of prime power orders using Dickson polynomials.
As with the classical Chebyshev polynomials, Dickson polynomials of the second kind have also been studied. These polynomials of degree  with parameter
with parameter  may be defined by
may be defined by
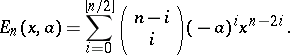 |
Dickson polynomials of the second kind satisfy the same recurrence as those of the first kind, except that the initial polynomial 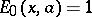 . See [a10], Chap. 2, for other basic properties of these polynomials.
. See [a10], Chap. 2, for other basic properties of these polynomials.
Contrary to the many known properties of the Dickson polynomials 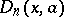 of the first kind, as indicated in [a10], very few properties of Dickson polynomials of the second kind are known (1998); see, for example, [a10], p. 76, as this comment relates to permutations.
of the first kind, as indicated in [a10], very few properties of Dickson polynomials of the second kind are known (1998); see, for example, [a10], p. 76, as this comment relates to permutations.
Dickson polynomials in several variables have been considered by a number of authors. For a brief survey see [a10], Sects. 2.4, 3.5, and 4.3. A connection of Dickson polynomials in several variables to circulant determinants is given in [a10], Sect. 7.8.
Dickson polynomials have been studied over a number of algebraic settings in addition to finite fields. In particular, various properties of Dickson polynomials have been obtained for the ring 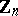 of integers modulo
of integers modulo  as well as for the Galois ring
as well as for the Galois ring 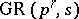 (a degree
(a degree  Galois extension of
Galois extension of 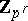 ), infinite algebraic extensions of finite fields, and matrix rings, see [a10], Chaps. 4; 5.
), infinite algebraic extensions of finite fields, and matrix rings, see [a10], Chaps. 4; 5.
References
| [a1] | D. Blessenohl, K. Johnsen, "Eine Verschärfung des Satzes von der Normalbasis" J. Algebra , 103 (1986) pp. 141–159 |
| [a2] | W.-S. Chou, J. Gomez-Calderon, G.L. Mullen, "Value sets of Dickson polynomials over finite fields" J. Number Th. , 30 (1988) pp. 334–344 |
| [a3] | S.D. Cohen, "Proof of a conjecture of Chowla and Zassenhaus on permutation polynomials" Canad. Math. Bull. , 33 (1990) pp. 230–234 |
| [a4] | L.E. Dickson, "The analytic representation of substitutions on a power of a prime number of letters with a discussion of the linear group" Ann. of Math. , 11 (1897) pp. 65–120; 161–183 |
| [a5] | M. Fried, "On a conjecture of Schur" Michigan Math. J. , 17 (1970) pp. 41–55 |
| [a6] | S. Gao, G.L. Mullen, "Dickson polynomials and irreducible polynomials over finite fields" J. Number Th. , 49 (1994) pp. 118–132 |
| [a7] | J. Gomez-Calderon, D.J. Madden, "Polynomials with small value sets over finite fields" J. Number Th. , 28 (1988) pp. 167–188 |
| [a8] | L.C. Hsu, G.L. Mullen, P.J.-S. Shiue, "Dickson–Stirling numbers" Proc. Edinburgh Math. Soc. , 40 (1997) pp. 409–423 |
| [a9] | R. Lidl, G.L. Mullen, "The world's most interesting class of integral polynomials" Preprint (1999) |
| [a10] | R. Lidl, G.L. Mullen, G. Turnwald, "Dickson Polynomials" , Pitman Monogr. Surveys Pure Appl. Math. , 65 , Longman (1993) |
| [a11] | R. Lidl, H. Niederreiter, "Finite fields" , Encycl. Math. Appl. , 20 , Cambridge Univ. Press (1997) |
| [a12] | W.H. Mills, "Polynomials with minimal value sets" Pacific J. Math. , 14 (1964) pp. 225–241 |
| [a13] | G.L. Mullen, "Permutation polynomials: A matrix analogue of Schur's conjecture and a survey of recent results" Finite Fields Appl. , 1 (1995) pp. 242–258 |
| [a14] | K.V.H. Parshall, "A study in group theory: Leonard Eugene Dickson's "Linear Groups" " Math. Intelligencer , 13 : 1 (1991) pp. 7–11 |
| [a15] | A. Scheerhorn, "Dickson polynomials and completely normal elements over finite fields" D. Gollmann (ed.) , Applications of Finite Fields , IMA Conf. Proc. Ser. , Oxford Univ. Press (1996) pp. 47–55 |
| [a16] | I. Schur, "Über den Zusammenhang zwischen einem Problem der Zahlentheorie und einem Satz über algebraische Funktionen" Sitzungsber. Preuss. Akad. Wiss. Berlin (1923) pp. 123–134 |
| [a17] | G. Turnwald, "On Schur's conjecture" J. Austral. Math. Soc. Ser. A , 58 (1995) pp. 312–357 |
| [a18] | K.S. Williams, "A generalization of Cardan's solution of the cubic" Math. Gaz. , 46 (1962) pp. 221–223 |
Dickson polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dickson_polynomial&oldid=16913