Dickman-function(2)
From Encyclopedia of Mathematics
The unique continuous solution of the system
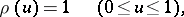 |
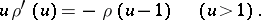 |
The Dickman function 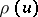 occurs in the problem of estimating the number
occurs in the problem of estimating the number 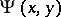 of positive integers not exceeding
of positive integers not exceeding  that are free of prime factors greater than
that are free of prime factors greater than 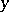 : for any fixed
: for any fixed 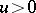 , one has
, one has  as
as 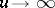 [a2], [a4].
[a2], [a4].
The function 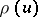 is positive, non-increasing and tends to zero at a rate faster than exponential as
is positive, non-increasing and tends to zero at a rate faster than exponential as 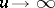 . A precise asymptotic estimate is given by the de Bruijn–Alladi formula [a1], [a3]:
. A precise asymptotic estimate is given by the de Bruijn–Alladi formula [a1], [a3]:
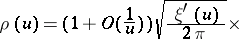 |
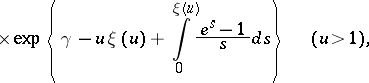 |
where 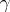 is the Euler constant and
is the Euler constant and  is the unique positive solution of the equation
is the unique positive solution of the equation 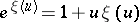 .
.
References
| [a1] | K. Alladi, "The Turán–Kubilius inequality for integers without large prime factors" J. Reine Angew. Math. , 335 (1982) pp. 180–196 |
| [a2] | N.G. de Bruijn, "On the number of positive integers 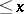 and free of prime factors and free of prime factors 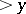 " Nederl. Akad. Wetensch. Proc. Ser. A , 54 (1951) pp. 50–60 " Nederl. Akad. Wetensch. Proc. Ser. A , 54 (1951) pp. 50–60 |
| [a3] | N.G. de Bruijn, "The asymptotic behaviour of a function occurring in the theory of primes" J. Indian Math. Soc. (N.S.) , 15 (1951) pp. 25–32 |
| [a4] | A. Hildebrand, G. Tenenbaum, "Integers without large prime factors" J. de Théorie des Nombres de Bordeaux , 5 (1993) pp. 411–484 |
How to Cite This Entry:
Dickman-function(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dickman-function(2)&oldid=15579
Dickman-function(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dickman-function(2)&oldid=15579
This article was adapted from an original article by A. Hildebrand (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article