Dichotomy method
method of division in halves
A method for numerically solving equations in a single unknown. Consider the equation 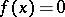 with a continuous function
with a continuous function  on the interval
on the interval  which takes values of different signs at the end points of the interval and which has a single root
which takes values of different signs at the end points of the interval and which has a single root  within
within  . To find
. To find  approximately, one divides
approximately, one divides  into halves and calculates the value of
into halves and calculates the value of  at the midpoint
at the midpoint  . If
. If  , one takes the two intervals
, one takes the two intervals 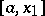 and
and 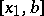 and from them selects for the next dichotomy the one at the end points of which the values of the function differ in sign. This continued division into halves gives a sequence
and from them selects for the next dichotomy the one at the end points of which the values of the function differ in sign. This continued division into halves gives a sequence 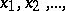 which converges to the root
which converges to the root 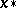 with the rate of a geometrical progression:
with the rate of a geometrical progression:
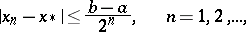 | (1) |
where the bound (1) cannot be improved upon in this class of functions. If 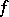 has more than one root in
has more than one root in  , the sequence will converge to one of them.
, the sequence will converge to one of them.
A method for minimizing a function of one variable. One has to find the minimum
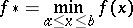 |
of a unimodal function 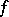 on an interval
on an interval  and to determine the point
and to determine the point  at which it is attained. For this, one divides
at which it is attained. For this, one divides  into halves and near the middle
into halves and near the middle  calculates the values of
calculates the values of 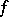 at the two points
at the two points  and
and  , where the number
, where the number  is a parameter of the method and is sufficiently small. Then the values
is a parameter of the method and is sufficiently small. Then the values 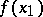 and
and 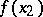 are compared, and on the basis that
are compared, and on the basis that  is unimodal one selects from the two intervals
is unimodal one selects from the two intervals  and
and  the one that certainly contains
the one that certainly contains 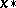 . For example, if
. For example, if  , this will be
, this will be  , otherwise
, otherwise 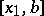 . The interval is again divided into halves, and near the middle
. The interval is again divided into halves, and near the middle  one takes two points
one takes two points 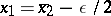 and
and  , compares the values of the function, etc. As a result, one obtains a sequence of midpoints
, compares the values of the function, etc. As a result, one obtains a sequence of midpoints 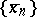 for which
for which
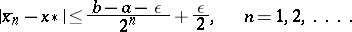 | (2) |
As an approximation to 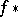 the value
the value 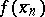 for sufficiently large
for sufficiently large  is taken.
is taken.
The name is given to the method because at each step in this algorithm the segment containing the minimum becomes approximately half the length. The dichotomy method is not the best in the class of unimodal functions. There are more effective methods that enable one to use the same number of calculations on the values of the function to obtain an accuracy better than that of (2) (see, for example, the Fibonacci method).
References
| [1] | B.P. Demidovich, I.A. Maron, "Foundations of computational mathematics" , Moscow (1966) (In Russian) |
| [2] | D.J. Wilde, "Optimum seeking methods" , Prentice-Hall (1964) |
Comments
The first example of the two dichotomy methods described above is known as the bisection method in the English literature. It is the classical example of an enclosure method (a two-sided method). Since its convergence is fairly slow, one has tried to device more rapidly converging methods. One such method which is often (but not always) faster than the bisection method and whose convergence is also guaranteed, is the Regula Falsi method (method of false position, see, e.g., [a1]). A modification of this method that avoids the disadvantage of the Regula Falsi method is a method of H. Brent [a2], which is based on an earlier algorithm of T. Dekker [a3].
A unimodal function on an interval is a function having only one extremum within the interval.
References
| [a1] | K.E. Atkinson, "An introduction to numerical analysis" , Wiley (1978) |
| [a2] | H. Brent, "Algorithms for minimization without derivatives" , Prentice-Hall (1973) |
| [a3] | T. Dekker, "Finding a zero by successive linear interpolation" B. Dejon (ed.) P. Henrici (ed.) , Constructive aspects of the fundamental theorem of algebra , Wiley (1969) pp. 37–48 |
Dichotomy method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dichotomy_method&oldid=12591