Dichotomy
From Encyclopedia of Mathematics
The property that for a linear system of ordinary differential equations
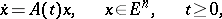 |
with bounded continuous coefficients, there are positive constants 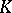 ,
, 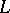 ,
, 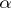 , and
, and 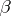 such that there exists a decomposition
such that there exists a decomposition  for which
for which
 |
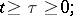 |
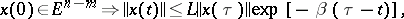 |
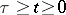 |
(exponential dichotomy; if 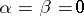 , one has ordinary dichotomy). The presence of exponential dichotomy is equivalent to saying that the inhomogeneous system
, one has ordinary dichotomy). The presence of exponential dichotomy is equivalent to saying that the inhomogeneous system
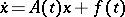 |
has, for any bounded continuous function 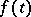 ,
, 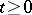 , at least one bounded solution on
, at least one bounded solution on 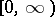 [1]. The theory of dichotomy [2], transferred to equations in Banach spaces, is also employed in the study of flows and cascades on smooth manifolds [4].
[1]. The theory of dichotomy [2], transferred to equations in Banach spaces, is also employed in the study of flows and cascades on smooth manifolds [4].
References
| [1] | O. Perron, "Stability of differential equations" Math. Z. , 32 : 5 (1930) pp. 703–728 |
| [2] | H.H. Scheffer, "Linear differential equations and function spaces" , Acad. Press (1966) |
| [3] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [4] | D.V. Anosov, "Geodesic flows on closed Riemann manifolds with negative curvature" Proc. Steklov Inst. Math. , 90 (1969) Trudy Mat. Inst. Steklov. , 90 (1967) |
Comments
References
| [a1] | V.I. Oseledec, "A multiplicative ergodic theorem. Characteristic Lyapunov numbers for dynamical systems" Trans. Moscow Math. Soc. , 19 (1969) pp. 197–232 Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 179–210 |
How to Cite This Entry:
Dichotomy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dichotomy&oldid=12757
Dichotomy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dichotomy&oldid=12757
This article was adapted from an original article by R.A. Prokhorova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article