Diagram(2)
Let  and
and  be directed graphs (also called oriented graphs, diagram schemes or pre-categories; cf. also Graph, oriented). A diagram of shape (also called a diagram of type)
be directed graphs (also called oriented graphs, diagram schemes or pre-categories; cf. also Graph, oriented). A diagram of shape (also called a diagram of type)  in
in  is a morphism of graphs
is a morphism of graphs  ; i.e. if
; i.e. if  and
and  are given by
are given by
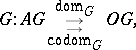 |
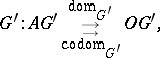 |
(here 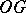 and
and 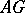 denote, respectively, a set of objects and a set of arrows of
denote, respectively, a set of objects and a set of arrows of  ), then a morphism
), then a morphism 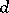 is a pair of mappings
is a pair of mappings
 |
with 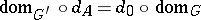 ,
, 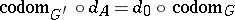 .
.
A diagram is called finite if its shape is a finite graph, i.e. 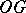 and
and  are finite sets. A diagram in a category
are finite sets. A diagram in a category 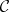 is defined as a diagram
is defined as a diagram  , where
, where 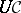 denotes the underlying graph of
denotes the underlying graph of 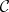 (with the same objects and arrows, forgetting which arrows are composites and which are identities).
(with the same objects and arrows, forgetting which arrows are composites and which are identities).
Every functor 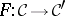 is also a diagram
is also a diagram  between the corresponding graphs. This observation defines the forgetful functor
between the corresponding graphs. This observation defines the forgetful functor 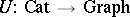 from small categories to small graphs (cf. also Functor).
from small categories to small graphs (cf. also Functor).
Let 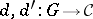 be two diagrams of the same shape
be two diagrams of the same shape 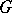 in the same category
in the same category 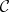 . A morphism between
. A morphism between 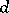 and
and  is a mapping
is a mapping 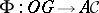 that carries each object
that carries each object 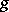 of the graph
of the graph 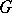 to an arrow
to an arrow 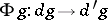 , such that for any arrow
, such that for any arrow 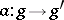 of
of 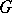 the diagram
the diagram
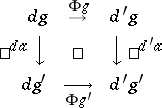 |
commutes.
All diagrams of the shape 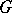 in
in 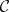 and all morphisms between them form a category.
and all morphisms between them form a category.
Let 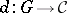 be a diagram in the category
be a diagram in the category 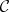 and let
and let 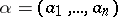 be a finite sequence of arrows of the graph
be a finite sequence of arrows of the graph 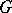 with
with 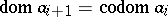 ,
,  . Put
. Put 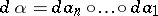 . A diagram
. A diagram  is called commutative if
is called commutative if 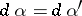 for any finite sequence
for any finite sequence 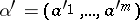 in
in 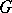 with
with 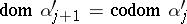 ,
,  ,
, 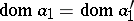 ,
, 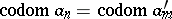 .
.
A sequence is a diagram  , where
, where 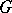 is of the form
is of the form
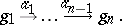 |
The corresponding diagram is represented by
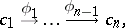 |
where 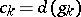 are objects and
are objects and  are arrows of
are arrows of 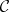 .
.
A triangle diagram in the category  is a diagram with shape graph
is a diagram with shape graph
 |
and is represented as
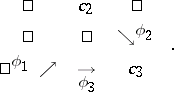 |
Commutativity means that  .
.
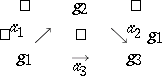
A quadratic diagram (also called a square diagram) in  corresponds to the graph
corresponds to the graph
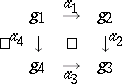 |
and is represented as
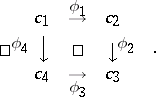 |
Commutativity means  .
.
References
| [a1] | P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967) |
| [a2] | A. Grothendieck, "Sur quelques points d'algebre homologique" Tôhoku Math. J. Ser. II , 9 (1957) pp. 120–221 |
| [a3] | S. Maclane, "Categories for the working mathematician" , Springer (1971) |
Diagram(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagram(2)&oldid=12484