Diagram
in a category 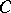
A mapping 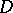 of an oriented graph
of an oriented graph 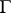 with set of vertices
with set of vertices 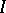 and set of edges
and set of edges 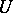 into the category
into the category 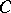 for which
for which
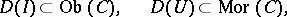 |
and  if the edge
if the edge 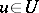 has source (origin)
has source (origin) 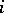 and target (end)
and target (end) 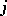 . The concept of a diagram in
. The concept of a diagram in 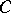 may also be defined as the image of the mapping
may also be defined as the image of the mapping 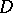 , in order to obtain a better visualization of diagrams.
, in order to obtain a better visualization of diagrams.
Let 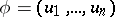 be an oriented chain of the graph
be an oriented chain of the graph 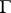 with source
with source  and target
and target 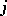 , i.e. a non-empty finite sequence of edges in which the source of each edge coincides with the target of the preceding one; also, let
, i.e. a non-empty finite sequence of edges in which the source of each edge coincides with the target of the preceding one; also, let 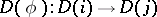 denote the composition of morphisms
denote the composition of morphisms
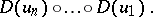 |
The diagram 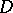 is said to be commutative if
is said to be commutative if 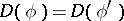 for any two oriented chains
for any two oriented chains 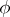 and
and  with identical source and target.
with identical source and target.
The most frequently encountered forms of diagrams are sequences, triangular diagrams and square diagrams. To define a sequence, the defining graph is taken to have the form
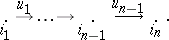 |
The corresponding diagram is represented as follows:
 |
where the 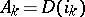 are objects in the category
are objects in the category 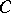 , while the
, while the 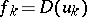 are morphisms in this category.
are morphisms in this category.
A triangular diagram in a category 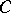 corresponds to the graph
corresponds to the graph
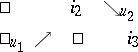 |
and is represented as follows:
 |
Commutativity of this diagram means that 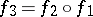 .
.
A square diagram corresponds to the graph
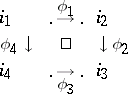 |
and is represented as follows:
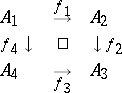 |
Commutativity of this diagram means that 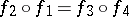 .
.
The class of diagrams with a given graph 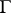 forms a category. A morphism of a diagram
forms a category. A morphism of a diagram 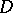 into a diagram
into a diagram 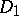 is taken to be a family of morphisms
is taken to be a family of morphisms 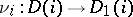 , where
, where 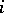 runs through the set of vertices of
runs through the set of vertices of 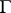 , so that for any edge
, so that for any edge  with source
with source  and target
and target 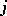 the condition
the condition 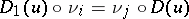 is met. In particular, one may speak of isomorphic diagrams. The graph
is met. In particular, one may speak of isomorphic diagrams. The graph 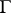 is sometimes referred to as the scheme of a diagram in
is sometimes referred to as the scheme of a diagram in 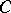 .
.
References
| [1] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221 |
Comments
References
| [a1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 |
Diagram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagram&oldid=46644