Descriptive set theory
The branch of set theory whose subject is the study of sets in dependence of those operations by which these sets may be constructed from relatively simple sets (e.g. closed or open subsets of a given Euclidean, metric or topological space). These operations include union, intersection, taking a complement or projection, etc. Descriptive set theory was created in the early 20th century by the studies of E. Borel, R. Baire and H. Lebesgue in connection with the measurability of sets. Borel-measurable sets received the name of Borel sets or 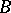 -sets (cf. Borel set). On the other hand, Baire proposed a classification of functions, in so-called Baire function classes, and proved a number of theorems concerning these functions (cf. Baire classes; Baire theorem). Lebesgue showed that
-sets (cf. Borel set). On the other hand, Baire proposed a classification of functions, in so-called Baire function classes, and proved a number of theorems concerning these functions (cf. Baire classes; Baire theorem). Lebesgue showed that 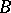 -sets are identical to Lebesgue sets of Baire functions (cf. Lebesgue set), gave the first classification of
-sets are identical to Lebesgue sets of Baire functions (cf. Lebesgue set), gave the first classification of 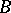 -sets and showed that none of its classes was empty.
-sets and showed that none of its classes was empty.
The study of 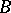 -sets became an important task of descriptive set theory, and the first such problem was the cardinality of
-sets became an important task of descriptive set theory, and the first such problem was the cardinality of 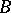 -sets. After the introduction of the Lebesgue measure it was found that the class of measurable sets is much wider than the class of
-sets. After the introduction of the Lebesgue measure it was found that the class of measurable sets is much wider than the class of 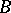 -sets, and there arose the problem of determining whether or not a given set is measurable. The solution of this problem for a particular set usually involves the classification of the process by which this set may be constructed, i.e. its descriptive structure. This defines another important circle of problems dealt with by descriptive set theory, viz., to find the widest possible class (with preservation of measurability) of operations over sets and the study of the properties of the results of these operations. The solution of these problems, which arose as a results of studies by French mathematicians, must be credited, in essence, to Russian mathematicians, viz. N.N. Luzin and his school.
-sets, and there arose the problem of determining whether or not a given set is measurable. The solution of this problem for a particular set usually involves the classification of the process by which this set may be constructed, i.e. its descriptive structure. This defines another important circle of problems dealt with by descriptive set theory, viz., to find the widest possible class (with preservation of measurability) of operations over sets and the study of the properties of the results of these operations. The solution of these problems, which arose as a results of studies by French mathematicians, must be credited, in essence, to Russian mathematicians, viz. N.N. Luzin and his school.
One of the most important problems, viz. the problem of the cardinality of 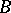 -sets, was solved by P.S. Aleksandrov [1] in 1916, who constructed the
-sets, was solved by P.S. Aleksandrov [1] in 1916, who constructed the 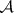 -operation for this purpose. He showed that the use of the
-operation for this purpose. He showed that the use of the 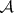 -operation, while taking intervals as the starting point, makes it possible to construct any desired
-operation, while taking intervals as the starting point, makes it possible to construct any desired 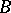 -set, and that any uncountable set obtained by way of the
-set, and that any uncountable set obtained by way of the 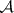 -operation (and called an
-operation (and called an 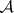 -set) contains a perfect set and thus has the cardinality of the continuum. This result was also independently obtained by F. Hausdorff. M.Ya. Suslin [2] showed that there exists an
-set) contains a perfect set and thus has the cardinality of the continuum. This result was also independently obtained by F. Hausdorff. M.Ya. Suslin [2] showed that there exists an 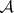 -set which is not a Borel set. He also introduced the name
-set which is not a Borel set. He also introduced the name 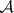 -set and
-set and  -operation, in honour of Aleksandrov.
-operation, in honour of Aleksandrov.  -sets are also known as Suslin sets, or as analytic sets (cf. Analytic set). For an
-sets are also known as Suslin sets, or as analytic sets (cf. Analytic set). For an 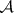 -set to be a
-set to be a 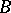 -set it is necessary and sufficient: 1) for its complement to be again an
-set it is necessary and sufficient: 1) for its complement to be again an 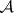 -set (the Suslin criterion); or 2) for it to be the result of an
-set (the Suslin criterion); or 2) for it to be the result of an 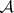 -operation with non-intersecting components (the Luzin criterion). All
-operation with non-intersecting components (the Luzin criterion). All 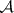 -sets are measurable and display the Baire property. The following new methods for obtaining
-sets are measurable and display the Baire property. The following new methods for obtaining 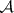 -sets, equivalent to
-sets, equivalent to 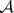 -operations, were found:
-operations, were found: 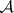 -sets are projections of
-sets are projections of 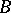 -sets (and even of
-sets (and even of 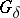 -sets);
-sets); 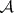 -sets are continuous images of the space
-sets are continuous images of the space  of irrational numbers; and, as a consequence,
of irrational numbers; and, as a consequence, 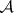 -sets are continuous images of
-sets are continuous images of 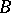 -sets [3]. At the same time, a continuous one-to-one (and even a countably-to-multiple [4]) image of a
-sets [3]. At the same time, a continuous one-to-one (and even a countably-to-multiple [4]) image of a 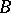 -set is a
-set is a 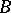 -set, and any uncountable
-set, and any uncountable 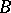 -set is the union of an at most countable set and a one-to-one continuous image of
-set is the union of an at most countable set and a one-to-one continuous image of  [3]. Finally, Luzin found yet another important way of defining
[3]. Finally, Luzin found yet another important way of defining 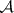 -sets with the aid of his sieve operation (cf. Luzin sieve). Transfinite sieve indices and constituents have become a powerful tool in the study of the properties of
-sets with the aid of his sieve operation (cf. Luzin sieve). Transfinite sieve indices and constituents have become a powerful tool in the study of the properties of 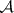 -sets and their complements:
-sets and their complements: 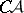 -sets (cf.
-sets (cf. 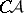 -set).
-set).
In the course of his studies on the cardinality of 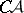 -sets, Luzin introduced projective sets (cf. Projective set). Each class
-sets, Luzin introduced projective sets (cf. Projective set). Each class 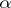 of projective sets contains sets which do not belong to classes
of projective sets contains sets which do not belong to classes 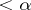 [3], [5]. The concept of a universal set [3], [6], [5] is an important tool in the demonstration of this and other theorems asserting that certain classes of sets are non-empty. The study of projective sets, even those of the second class, encounters difficulties which have not yet been overcome. One problem which has thus remained unsolved is the measurability of
[3], [5]. The concept of a universal set [3], [6], [5] is an important tool in the demonstration of this and other theorems asserting that certain classes of sets are non-empty. The study of projective sets, even those of the second class, encounters difficulties which have not yet been overcome. One problem which has thus remained unsolved is the measurability of 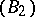 -sets, the cardinality of these sets, and whether or not they display the Baire property. Important results in this matter were obtained by P.S. Novikov [4]: There exists an uncountable
-sets, the cardinality of these sets, and whether or not they display the Baire property. Important results in this matter were obtained by P.S. Novikov [4]: There exists an uncountable 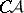 -set for which the assumption that it contains no perfect subset is not self-contradictory; there exists a
-set for which the assumption that it contains no perfect subset is not self-contradictory; there exists a 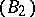 -set for which the assumption that it is non-measurable is not self-contradictory.
-set for which the assumption that it is non-measurable is not self-contradictory.
The introduction by Aleksandrov [7] of the 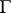 -operation, which is complementary to the
-operation, which is complementary to the 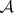 -operation, was the first step in the development of A.N. Kolmogorov's [8] and Hausdorff's [9] general theory of set-theoretic operations; however, the fundamental class of operations is constituted by positive set-theoretic operations, or the so-called
-operation, was the first step in the development of A.N. Kolmogorov's [8] and Hausdorff's [9] general theory of set-theoretic operations; however, the fundamental class of operations is constituted by positive set-theoretic operations, or the so-called 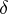 -
-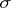 -operations. For each such
-operations. For each such 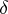 -
-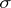 -operation
-operation 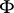 a complementary
a complementary 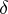 -
-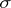 -operation
-operation 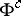 was defined and the formula
was defined and the formula
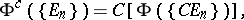 |
which may be considered as the definition of 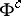 , was given. The concept of a normal
, was given. The concept of a normal 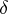 -
-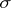 -operation (for any family
-operation (for any family 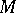 of sets
of sets 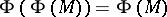 [8]) was also introduced. The
[8]) was also introduced. The 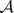 -operation and the
-operation and the  -operation are mutually complementary normal
-operation are mutually complementary normal 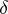 -
-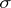 -operations. The same applies to the operations of countable union and countable intersection. One of the key theorems of the general theory of operations over sets in topological spaces is Kolmogorov's complements theorem: If a space contains a discontinuum, if
-operations. The same applies to the operations of countable union and countable intersection. One of the key theorems of the general theory of operations over sets in topological spaces is Kolmogorov's complements theorem: If a space contains a discontinuum, if 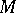 is the system of all closed subsets of this space and if
is the system of all closed subsets of this space and if 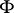 is an arbitrary set-theoretic operation, then the complement of at least one set of the family
is an arbitrary set-theoretic operation, then the complement of at least one set of the family  does not belong to it [8], [5], [9]. The application to a given family
does not belong to it [8], [5], [9]. The application to a given family 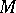 of sets of
of sets of 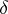 -
-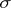 -operations
-operations 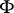 and
and 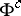 in alternation makes it possible to construct an increasing transfinite sequence of classes
in alternation makes it possible to construct an increasing transfinite sequence of classes 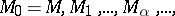
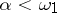 , which satisfies the Kolmogorov theorem on non-emptyness of classes: If
, which satisfies the Kolmogorov theorem on non-emptyness of classes: If 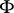 is a normal
is a normal 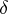 -
-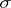 -operation of greater cardinality than the operation of countable union (or of countable intersection), while
-operation of greater cardinality than the operation of countable union (or of countable intersection), while 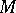 is the family of all closed subsets of a metric space containing a discontinuum, then all the classes
is the family of all closed subsets of a metric space containing a discontinuum, then all the classes 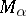 ,
, 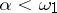 , generated by the operation
, generated by the operation  from the family
from the family 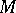 are pairwise different. Here, a
are pairwise different. Here, a 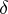 -
- -operation
-operation  is considered to be of greater cardinality than a
is considered to be of greater cardinality than a 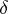 -
-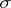 -operation
-operation  if
if 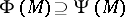 for any family
for any family  of sets [8], [5]. If
of sets [8], [5]. If 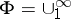 (or
(or 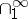 ), then the classes
), then the classes  ,
, 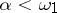 , generated by the operation
, generated by the operation 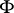 on the family
on the family 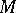 represent the classes of
represent the classes of 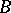 -sets generated by the family
-sets generated by the family 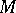 (the Hausdorff classification). In a similar manner, an
(the Hausdorff classification). In a similar manner, an  -operation generates classes
-operation generates classes 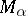 ,
, 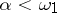 , of
, of 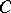 -sets (Luzin sets, cf. Luzin set) out of the family
-sets (Luzin sets, cf. Luzin set) out of the family 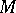 of Borel sets. All
of Borel sets. All 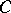 -sets are measurable and have the Baire property. All
-sets are measurable and have the Baire property. All 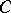 -sets form part of the class
-sets form part of the class 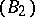 , but do not exhaust it.
, but do not exhaust it.
The concept of separation [4], introduced by Luzin, plays a highly important part in descriptive set theory. The first separation principle: Any two non-intersecting 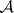 -sets are
-sets are 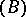 separable. The second separation principle: If
separable. The second separation principle: If  and
and 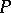 are two
are two  -sets (or
-sets (or 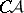 -sets), then the sets
-sets), then the sets 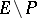 and
and 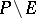 are (
are ( ) separable. There exists two
) separable. There exists two 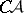 -sets which are not
-sets which are not 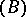 separable. The problem of separation of second-class projective sets was solved by Novikov [4] and its separation principles are invertible: they are obtained from the respective theorems for projective sets of the first class by replacing
separable. The problem of separation of second-class projective sets was solved by Novikov [4] and its separation principles are invertible: they are obtained from the respective theorems for projective sets of the first class by replacing 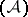 by
by 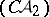 ,
,  by
by 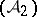 and
and 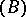 by
by 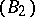 . Novikov [4] also solved the separation problem in the class of
. Novikov [4] also solved the separation problem in the class of 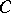 -sets (see also [3]). He also generalized the concept of separation of sets to include the concept of simultaneous or multiple separation of sets, as well as the principle of equality of indices [4], which is a principal instrument in proving the theorems on multiple separation.
-sets (see also [3]). He also generalized the concept of separation of sets to include the concept of simultaneous or multiple separation of sets, as well as the principle of equality of indices [4], which is a principal instrument in proving the theorems on multiple separation.
An important stage in the development of descriptive set theory was the solution of the uniformization problem. A set  uniformizes a set
uniformizes a set 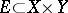 if
if  , if
, if  has the same projection on
has the same projection on 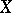 as does
as does 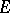 and if it is projected on
and if it is projected on 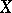 in a one-to-one manner. All
in a one-to-one manner. All  -sets are uniformized by
-sets are uniformized by 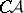 -sets. The process of effective selection of a point [4] in a non-empty
-sets. The process of effective selection of a point [4] in a non-empty 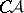 -set yielded a stronger result: All
-set yielded a stronger result: All 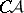 -sets are uniformized by a
-sets are uniformized by a 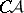 -set. Any
-set. Any 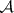 -set is uniformized by a set of type
-set is uniformized by a set of type 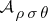 [3], [10]. There exists an
[3], [10]. There exists an 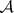 -set in the Euclidean plane which is not uniformized either by an
-set in the Euclidean plane which is not uniformized either by an 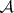 -set or by a
-set or by a 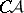 -set (see, for example, [11]). The problem of the conditions under which a
-set (see, for example, [11]). The problem of the conditions under which a 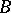 -set can be uniformized by a
-set can be uniformized by a 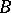 -set can be most generally answered as follows: Any plane
-set can be most generally answered as follows: Any plane 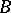 -set intersecting the straight lines
-set intersecting the straight lines 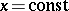 in
in 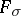 -sets is uniformized by a
-sets is uniformized by a 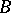 -set. The problem of uniformization arose in solving the problem of implicit
-set. The problem of uniformization arose in solving the problem of implicit 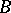 -functions [3]. Other problems arose at the same time: the nature of projections of
-functions [3]. Other problems arose at the same time: the nature of projections of 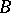 -sets, splitting of sets, covering of sets, and the nature of the set of all projection points of a given
-sets, splitting of sets, covering of sets, and the nature of the set of all projection points of a given 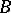 -set
-set 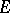 whose pre-images (in intersection with
whose pre-images (in intersection with 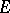 ) display a certain given property. The following theorems [3] give some idea of the second and third problems: a
) display a certain given property. The following theorems [3] give some idea of the second and third problems: a 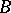 -set with a countable-to-multiple projection is the union of a countable number of uniform
-set with a countable-to-multiple projection is the union of a countable number of uniform 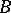 -sets and, for any two such sets, one of them will lie beneath the other (splitting theorem of a
-sets and, for any two such sets, one of them will lie beneath the other (splitting theorem of a 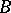 -set); any
-set); any 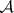 -set with a countable-to-multiple projection is contained in some
-set with a countable-to-multiple projection is contained in some 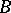 -set with this property (covering theorem of an
-set with this property (covering theorem of an  -set).
-set).
In addition to the Lebesgue and Hausdorff classification of  -sets, there is also their classification according to Luzin–de la Vallée Poussin. In this classification, the structure of sets of a given class
-sets, there is also their classification according to Luzin–de la Vallée Poussin. In this classification, the structure of sets of a given class 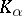 ,
, 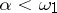 , is studied by means of sets which can be represented as an intersection but not as a union of a countable number of sets of classes
, is studied by means of sets which can be represented as an intersection but not as a union of a countable number of sets of classes 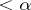 ; these sets are said to be elements of class
; these sets are said to be elements of class 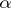 . Any set of class
. Any set of class 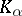 is the union of a countable number of pairwise non-intersecting elements of classes
is the union of a countable number of pairwise non-intersecting elements of classes 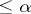 . Each class
. Each class 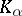 can be subdivided into subclasses
can be subdivided into subclasses 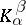 ,
, 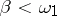 , each class containing subclasses with numbers
, each class containing subclasses with numbers  which may be arbitrarily large. Since each set of class
which may be arbitrarily large. Since each set of class 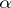 consists of elements, the problem arose of studying the elements themselves; in particular, of the presence in each class
consists of elements, the problem arose of studying the elements themselves; in particular, of the presence in each class 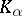 of a basic topological type of elements, to be called canonical, such that each element of class
of a basic topological type of elements, to be called canonical, such that each element of class 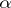 may be represented as the union of a countable number of canonical elements of classes
may be represented as the union of a countable number of canonical elements of classes 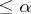 (everything being considered in the space
(everything being considered in the space  of irrational numbers). The first class includes canonical elements of two types: a one-point set and a topological image of a perfect Cantor set. Each element in the second class [12] is the union of a canonical element of class 2, which is a set homeomorphic to the space
of irrational numbers). The first class includes canonical elements of two types: a one-point set and a topological image of a perfect Cantor set. Each element in the second class [12] is the union of a canonical element of class 2, which is a set homeomorphic to the space  , and a set of class
, and a set of class 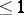 . Canonical elements of the third class have also been found; these canonical elements have been constructed by Baire [3]. The problem of existence of canonical elements of higher classes, which was very difficult, was solved by L.V. Keldysh [13], who proved that canonical elements exist in each class
. Canonical elements of the third class have also been found; these canonical elements have been constructed by Baire [3]. The problem of existence of canonical elements of higher classes, which was very difficult, was solved by L.V. Keldysh [13], who proved that canonical elements exist in each class 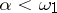 and clarified their structure. Each element of class
and clarified their structure. Each element of class 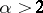 is the union of one canonical element of class
is the union of one canonical element of class 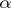 with at most a countable number of sets of classes
with at most a countable number of sets of classes 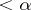 . Yet another difficult problem in this field is connected with the construction of arithmetical examples of
. Yet another difficult problem in this field is connected with the construction of arithmetical examples of 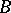 -sets of lower classes. Baire [3] gave such an example for the class 3. Keldysh [13] gave arithmetical examples of elements of all finite classes (see also [3]), and pointed to the possibility, in principle, of constructing such examples for classes
-sets of lower classes. Baire [3] gave such an example for the class 3. Keldysh [13] gave arithmetical examples of elements of all finite classes (see also [3]), and pointed to the possibility, in principle, of constructing such examples for classes 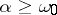 .
.
An important part in descriptive set theory is played by the Lavrent'ev theorem on the extension of homeomorphisms [9]: Let 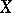 and
and 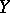 be complete metric spaces, let
be complete metric spaces, let 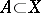 ,
, 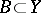 and let
and let 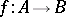 be a homeomorphism; then there exists an extension of
be a homeomorphism; then there exists an extension of 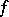 to a homeomorphism of two
to a homeomorphism of two 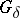 -subsets of these spaces. This theorem readily leads to the theorem of topological invariance [9]: Let
-subsets of these spaces. This theorem readily leads to the theorem of topological invariance [9]: Let 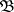 be a system of closed sets and let
be a system of closed sets and let 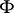 be a
be a 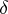 -
-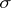 -operation such that intersection of a
-operation such that intersection of a 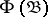 -set (i.e. of a set of the family
-set (i.e. of a set of the family 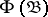 ) with a
) with a 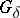 -set is again a
-set is again a 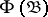 -set; then each
-set; then each 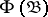 -subset of a complete metric space is a
-subset of a complete metric space is a 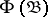 -set in any metric space in which it is topologically contained. In this theorem,
-set in any metric space in which it is topologically contained. In this theorem, 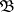 may be replaced by a system
may be replaced by a system 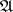 of open sets. Thus,
of open sets. Thus,  -sets for which
-sets for which 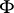 satisfies the above condition and which form part of complete metric spaces are absolute
satisfies the above condition and which form part of complete metric spaces are absolute 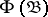 -sets, and the same applies to
-sets, and the same applies to 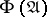 -sets (as regards the absolute nature in the class of metric spaces). In a number of special cases, such as
-sets (as regards the absolute nature in the class of metric spaces). In a number of special cases, such as 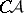 -sets [7] (
-sets [7] (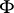 is a
is a 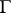 -operation), this result has been established without having recourse to Lavrent'ev's theorem. Any complete metric space is an absolute
-operation), this result has been established without having recourse to Lavrent'ev's theorem. Any complete metric space is an absolute 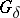 . Any metrizable absolute
. Any metrizable absolute 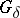 is homeomorphic to some complete metric space (the Aleksandrov–Hausdorff theorem [9]).
is homeomorphic to some complete metric space (the Aleksandrov–Hausdorff theorem [9]).
The following Aleksandrov–Urysohn theorem on the topological characterization of the space of irrational numbers is valid: Each zero-dimensional metric space  with a countable base which has no points of local compactness and which is an absolute
with a countable base which has no points of local compactness and which is an absolute 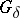 , is homeomorphic to the space
, is homeomorphic to the space  . Since
. Since  is an absolute
is an absolute 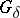 and has all the other properties of the space
and has all the other properties of the space 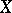 , it follows that the properties of
, it follows that the properties of 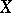 listed in the theorem represent a full topological characterization of
listed in the theorem represent a full topological characterization of  . This characterization led to the following result [14]: Any metric space which is a continuous image of
. This characterization led to the following result [14]: Any metric space which is a continuous image of  (and thus, an absolute
(and thus, an absolute 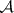 -set) is also a quotient image of
-set) is also a quotient image of  . One may also quote the following related results: A non-empty separable metric space is a continuous open image of
. One may also quote the following related results: A non-empty separable metric space is a continuous open image of  if and only if it is an absolute
if and only if it is an absolute 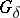 [15]; here, "open" may be replaced by "closed" . The concept of a
[15]; here, "open" may be replaced by "closed" . The concept of a 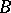 -measurable mapping or a
-measurable mapping or a 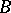 -function, in particular, of a
-function, in particular, of a 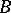 -measurable mapping of class
-measurable mapping of class 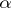 , is a generalization of a continuous mapping; the concepts of a generalized homeomorphism of class
, is a generalization of a continuous mapping; the concepts of a generalized homeomorphism of class 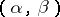 and of a
and of a 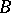 -isomorphism are generalizations of a homeomorphism. For such mappings see [6].
-isomorphism are generalizations of a homeomorphism. For such mappings see [6].
In formulating the results, the class of spaces to which they are applicable is usually not specified. This is explained by the fact that most of the classical results were obtained for subsets of  , but almost-all of them (save specified exceptions) remain valid if
, but almost-all of them (save specified exceptions) remain valid if  is replaced by any separable absolute
is replaced by any separable absolute 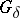 (in particular, by a complete metric space with a countable base). Further developments in descriptive set theory involved the generalization of the classical results to include the following cases: 1) complete metric spaces (not necessarily separable); 2) perfectly-normal topological spaces, including, in particular, compact Hausdorff spaces; and 3) general topological spaces. Even in the first case the generalization of the classical theory encounters serious difficulties, and is frequently altogether impossible. A.H. Stone [16] considered the generalization of the theory of
(in particular, by a complete metric space with a countable base). Further developments in descriptive set theory involved the generalization of the classical results to include the following cases: 1) complete metric spaces (not necessarily separable); 2) perfectly-normal topological spaces, including, in particular, compact Hausdorff spaces; and 3) general topological spaces. Even in the first case the generalization of the classical theory encounters serious difficulties, and is frequently altogether impossible. A.H. Stone [16] considered the generalization of the theory of 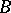 -sets and
-sets and 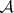 -sets to include this case.
-sets to include this case.
The class of perfectly-normal spaces is a class outside which the important fact that the system of 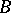 -sets (
-sets (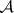 -sets) generated by the closed sets of the given space coincides with the system of
-sets) generated by the closed sets of the given space coincides with the system of 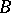 -sets (
-sets (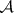 -sets) generated by the open sets of this space, is no longer true. The following important theorem on non-emptiness of classes [11] is valid: In any uncountable perfectly-normal compact Hausdorff space there exists for each class
-sets) generated by the open sets of this space, is no longer true. The following important theorem on non-emptiness of classes [11] is valid: In any uncountable perfectly-normal compact Hausdorff space there exists for each class 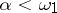 a
a 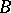 -set of class
-set of class 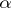 which is not a
which is not a 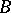 -set of class
-set of class 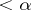 .
.
The problem of uniformization has become a partial case of the general problem on the section of a multi-valued mapping (cf. Section of a mapping).
The modern development of descriptive set theory in general topological spaces (third case) is connected with the needs of other domains of mathematics (e.g. potential theory). For more details see [17] (in which there is an extensive bibliography).
The ideas and methods of descriptive set theory had a profound effect on the development of several domains in mathematics: analysis, the theory of functions, topology, mathematical logic, etc.
References
| [1] | P.S. [P.S. Aleksandrov] Aleksandroff, "Sur la puissance des ensembles mésurables  " C.R. Acad. Sci. Paris , 162 (1916) pp. 323–325 " C.R. Acad. Sci. Paris , 162 (1916) pp. 323–325 |
| [2] | M.Ya. [M.Ya. Suslin] Souslin, "Sur une définition des ensembles measurables 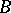 sans nombres transfinis" C.R. Acad. Sci. Paris , 164 (1917) pp. 88–90 sans nombres transfinis" C.R. Acad. Sci. Paris , 164 (1917) pp. 88–90 |
| [3] | N.N. [N.N. Luzin] Lusin, "Leçons sur les ensembles analytiques et leurs applications" , Gauthier-Villars (1930) |
| [4] | A.A. Lyapunov, "On P.S. Novikov's work in the field of descriptive set theory" Proc. Steklov Inst. Math. , 33 (1973) pp. 9–20 Trudy Mat. Inst. Steklov. , 133 (1973) pp. 11–22 |
| [5] | Yu.S. Ochan, "The theory of operations over sets" Uspekhi Mat. Nauk , 10 : 3 (1955) pp. 71–128 (In Russian) |
| [6] | K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French) |
| [7] | P.S. Aleksandrov, Fund. Math. , 5 (1924) pp. 160–165 |
| [8] | A.N. Kolmogorov, Mat. Sb. , 35 : 3–4 (1925) pp. 415–422 |
| [9] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [10] | A.A. [A.A. Lyapunov] Ljapunow, E.A. [E.A. Shchegolkov] Stschegolkow, W.J. [V.Ya. Arsenin] Arsenin, "Arbeiten zur deskriptiven Mengenlehre" , Deutsch. Verlag Wissenschaft. (1955) (Translated from Russian) |
| [11] | V.I. Ponomarev, "Borel sets in perfectly normal bicompacta" Soviet Math. Dokl. , 7 : 5 (1966) pp. 1236–12 Dokl. Akad. Nauk SSSR , 170 : 3 (1966) pp. 520–523 |
| [12] | P.S. Aleksandrov, P.S. Urysohn, "Ueber nulldimensionalen Punktmengen" Math. Ann. , 98 (1927) pp. 89–106 |
| [13] | L.V. Keldysh, Trudy Mat. Inst. Steklov. , 17 (1945) pp. 1–76 |
| [14] | E. Michael, A.H. Stone, "Quotients of the space of irrationals" Pacific J. Math. , 28 : 3 (1969) pp. 629–633 |
| [15] | A.V. Arkhangel'skii, "Open and near open mappings. Connections between spaces" Trans. Moscow Math. Soc. , 15 (1966) pp. 204–250 Trudy Moskov. Mat. Obshch. , 15 (1966) pp. 181–223 |
| [16] | A.H. Stone, "Non-separable Borel sets II" General Topology and its Applications , 2 (1972) pp. 249–270 |
| [17] | Z. Frolik, "A survey of separable descriptive theory of sets and spaces" Czechoslovak. Math. , 20 (1970) pp. 406–467 |
Comments
First some remarks on a supplementary list of references are presented, then precisions on the various commonly used terminologies and notations, and some complementation to the matter of the article, in which in particular three major events which took place during "modern times" are touched upon: the linkage to the foundational issues of modern set theory, the maturation of a powerful effective descriptive set theory, and the opening of a large field of applications to analysis.
Concerning the classical period (roughly from 1917 to 1945), one may consult in addition to [3], [6], [9], and [10], reference [a1], which is a marvellous long dictionary article.
For the modern period one can add [a2]–[a11]. [a2], [a3], [a4], [a5], which all stay at the level of the first separation theorem, are useful for their numerous applications to other fields. [a10] discusses most of the aspects of the theory: the classical one with its extensions (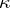 -analytic sets, various topological settings), and the effective one (see also [a11]). [a9] is a modern reference book, more directed to foundations than to applications: it covers in detail most of the classical and effective theories. [a6] is an excellent book in logic, which contains among many topics a chapter on descriptive set theory. [a8], in which some "generalized sieve" problems are solved, reveals the superiority of the effective methods over the classical ones. Finally [a7] is a recent example of what the modern theory can do in analysis.
-analytic sets, various topological settings), and the effective one (see also [a11]). [a9] is a modern reference book, more directed to foundations than to applications: it covers in detail most of the classical and effective theories. [a6] is an excellent book in logic, which contains among many topics a chapter on descriptive set theory. [a8], in which some "generalized sieve" problems are solved, reveals the superiority of the effective methods over the classical ones. Finally [a7] is a recent example of what the modern theory can do in analysis.
Now follow some important remarks about terminology and notations in the West:
A topological Hausdorff space homeomorphic to a complete metric separable space (i.e., a regular absolute 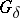 with countable base) is called a Polish space. Polish spaces have been and remain (in spite of generalizations) the natural frame of descriptive set theory. The fundamental Polish space
with countable base) is called a Polish space. Polish spaces have been and remain (in spite of generalizations) the natural frame of descriptive set theory. The fundamental Polish space  of irrationals is homeomorphic to the Baire space
of irrationals is homeomorphic to the Baire space 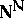 (often denoted by
(often denoted by 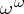 by the logicians who identify
by the logicians who identify 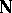 and the first infinite ordinal number
and the first infinite ordinal number 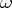 ).
).
Let 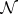 be short for the Baire space
be short for the Baire space 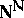 . A collection
. A collection 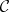 of subsets of
of subsets of 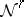 satisfies the reduction principle if for every pair
satisfies the reduction principle if for every pair 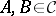 there are disjoint
there are disjoint 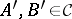 such that
such that 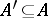 ,
, 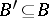 ,
, 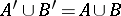 . The collection
. The collection 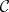 satisfies the separation principle if for every pair of disjoint
satisfies the separation principle if for every pair of disjoint 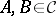 there exists an
there exists an 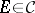 such that its complement
such that its complement 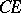 is also in
is also in 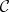 and
and 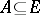 ,
, 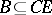 .
.
The 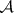 -operation is also called Suslin operation or Suslin scheme, and its results on a class
-operation is also called Suslin operation or Suslin scheme, and its results on a class 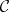 of sets are called the kernels of Suslin schemes on
of sets are called the kernels of Suslin schemes on 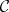 . When the surrounding space is Polish, kernels of Suslin schemes on closed (or Borel) sets coincide with the continuous images of
. When the surrounding space is Polish, kernels of Suslin schemes on closed (or Borel) sets coincide with the continuous images of  . For an arbitrary space
. For an arbitrary space 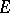 , the first construction gives "relative" analytic sets while the second one gives "absolute" ones. One generally uses "analytic" for one of the notions, and "Suslin" for the other; however, there are variations among the authors to decide which is which. Bourbaki [a2] made popular the notion of an absolute analytic (respectively, absolute Borel) space under the name of Suslin (respectively, Luzin) space; when one only considers the Borel structure of these spaces, one also finds Blackwell (respectively, standard) space.
, the first construction gives "relative" analytic sets while the second one gives "absolute" ones. One generally uses "analytic" for one of the notions, and "Suslin" for the other; however, there are variations among the authors to decide which is which. Bourbaki [a2] made popular the notion of an absolute analytic (respectively, absolute Borel) space under the name of Suslin (respectively, Luzin) space; when one only considers the Borel structure of these spaces, one also finds Blackwell (respectively, standard) space.
To denote the classes of the Borel hierarchy in a space 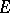 , one replaces more and more often the classical notations by the following ones:
, one replaces more and more often the classical notations by the following ones: 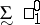 denotes the class
denotes the class 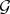 of open sets and
of open sets and 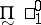 the class
the class 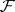 of closed sets;
of closed sets; 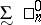 being defined,
being defined, 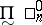 is its dual class (i.e. consists of the complements in
is its dual class (i.e. consists of the complements in 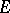 of the sets in
of the sets in 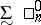 ) and
) and 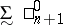 is the class of all countable unions of sets in
is the class of all countable unions of sets in 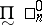 ; finally
; finally 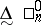 is the ambiguous class
is the ambiguous class 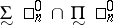 . So one has
. So one has 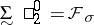 ,
, 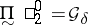 ,
, 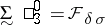 ,
, 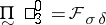 , etc. (cf. also Borel set of ambiguous class).
, etc. (cf. also Borel set of ambiguous class).
Similarly, for denoting the projective classes in a space 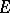 one uses the following notations:
one uses the following notations: 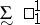 denotes the class
denotes the class 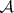 of analytic sets, projections on
of analytic sets, projections on 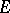 of the
of the 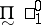 -subsets of
-subsets of 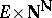 , whereas
, whereas 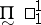 is the class
is the class  of co-analytic sets;
of co-analytic sets; 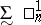 being defined,
being defined, 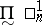 is its dual class and
is its dual class and 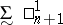 is the class of projections on
is the class of projections on 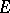 of
of 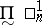 subsets of
subsets of 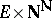 ; finally,
; finally, 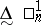 denotes the class
denotes the class 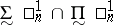 . So one has
. So one has 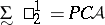 ,
, 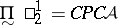 ,
, 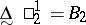 , etc.
, etc.
The letters 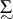 ,
, 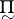 ,
, 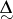 , denoting the classical classes of sets, are to be distinguished from the symbols
, denoting the classical classes of sets, are to be distinguished from the symbols 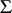 ,
, 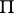 ,
, 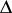 of their effective counterparts, which are now introduced (when
of their effective counterparts, which are now introduced (when  is a finite ordinal number). When
is a finite ordinal number). When 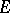 is Polish and is "reasonable" from the recursivity point of view (which is the case for all usual Polish spaces), one can distinguish inside
is Polish and is "reasonable" from the recursivity point of view (which is the case for all usual Polish spaces), one can distinguish inside 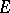 a countable family of simple open sets called effective or semi-recursive (or recursively enumerable in case
a countable family of simple open sets called effective or semi-recursive (or recursively enumerable in case 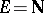 , cf. also Recursive set theory). This class, denoted by
, cf. also Recursive set theory). This class, denoted by 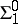 , shares enough closure properties, so one can define, as above, the hierarchies
, shares enough closure properties, so one can define, as above, the hierarchies 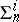 ,
, 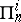 ,
,  , of effective classes, the operation of countable union being replaced by projection along
, of effective classes, the operation of countable union being replaced by projection along 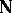 . All these classes are countable. However, if one defines, for each
. All these classes are countable. However, if one defines, for each 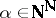 ,
, 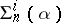 to be the class of all sets
to be the class of all sets 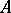 in
in 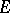 which occur as sections at
which occur as sections at 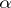 of a
of a 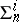 -set in
-set in 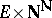 , and similarly for
, and similarly for 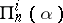 and
and 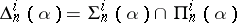 , these effective in
, these effective in 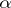 classes, which share properties similar to those of the effective classes, are related to the classical classes by the equalities:
classes, which share properties similar to those of the effective classes, are related to the classical classes by the equalities:
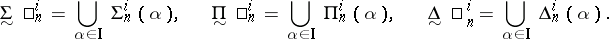 |
One then understands why the effective theory can be used to obtain "classical" results.
The classical part of descriptive set theory has been mainly created and developed by the Russian school between 1917 and 1945. However, during that period, major contributions to the subject have also come from the Polish and the Japanese school. Among the many members of the Polish school who worked on descriptive set theory, one must mention (at least): W. Sierpiński, among other things for his work with Luzin on the constituents of co-analytic sets (the Luzin–Sierpiński index is the model for the modern 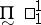 -norms); K. Kuratowski, in particular for his work on logical definitions and for the reduction theorem, the modern form of the second separation theorem (for every sequence
-norms); K. Kuratowski, in particular for his work on logical definitions and for the reduction theorem, the modern form of the second separation theorem (for every sequence  of
of 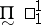 -sets there exists a sequence
-sets there exists a sequence 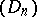 of disjoint
of disjoint 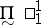 -sets with
-sets with 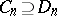 and
and 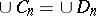 ); W. Hurewicz, for his characterization of
); W. Hurewicz, for his characterization of 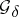 -sets among co-analytic sets, and of
-sets among co-analytic sets, and of 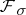 -sets among analytic sets (the origin of many recent works) and for the first explicit natural examples of co-analytic non-Borel sets (the set of all countable compact subsets of
-sets among analytic sets (the origin of many recent works) and for the first explicit natural examples of co-analytic non-Borel sets (the set of all countable compact subsets of 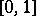 and the set of all compact subsets of the rationals of
and the set of all compact subsets of the rationals of 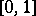 ); finally, S. Mazurkiewicz, for his pioneering work on Polish spaces and his natural example of a co-analytic non-Borel set (the set of everywhere-differentiable functions on
); finally, S. Mazurkiewicz, for his pioneering work on Polish spaces and his natural example of a co-analytic non-Borel set (the set of everywhere-differentiable functions on 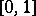 ). From the more recent (and smaller in size) Japanese school one must mention: Kunugui, whose work on Borel sets in product spaces is, with those of Novikov and V.Ya. Arsenin, at the origin of [a8]; and especially Kondô, who proved in 1937 that every co-analytic set in a product can be uniformized by a co-analytic graph (a result which can also be derived from an earlier selection result of Novikov, as was proved in the 1960s by J.W. Addison, one of the logicians who linked the classical theory to the effective theory independently developed by S.C. Kleene on
). From the more recent (and smaller in size) Japanese school one must mention: Kunugui, whose work on Borel sets in product spaces is, with those of Novikov and V.Ya. Arsenin, at the origin of [a8]; and especially Kondô, who proved in 1937 that every co-analytic set in a product can be uniformized by a co-analytic graph (a result which can also be derived from an earlier selection result of Novikov, as was proved in the 1960s by J.W. Addison, one of the logicians who linked the classical theory to the effective theory independently developed by S.C. Kleene on 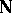 ).
).
All the important questions about projective sets which remained unsolved in the classical theory (cardinality of 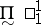 -sets, measurability of projective sets, etc.) have received satisfactory answers during the last three decades: they cannot be solved within the usual framework of set theory, but are related to each other and can be solved "positively" by adding new and natural axioms. Proofs rely on one hand on the sophisticated tools of axiomatic set theory, Gödel's constructible universe and it's inner models extensions (cf. Gödel constructive set), and the forcing method of P. Cohen, and, on the other hand, on a notion of infinite game which is now central in descriptive set theory (see [a9] for historical comments about this notion). In this canonical form, a game
-sets, measurability of projective sets, etc.) have received satisfactory answers during the last three decades: they cannot be solved within the usual framework of set theory, but are related to each other and can be solved "positively" by adding new and natural axioms. Proofs rely on one hand on the sophisticated tools of axiomatic set theory, Gödel's constructible universe and it's inner models extensions (cf. Gödel constructive set), and the forcing method of P. Cohen, and, on the other hand, on a notion of infinite game which is now central in descriptive set theory (see [a9] for historical comments about this notion). In this canonical form, a game 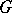 is a subset of
is a subset of  ; in a run of the game, two players I and II alternately choose integers (knowing the previous choices) so that at the end of the run they produce an element
; in a run of the game, two players I and II alternately choose integers (knowing the previous choices) so that at the end of the run they produce an element 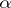 of
of 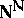 ; I wins the run if
; I wins the run if 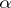 belongs to
belongs to 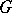 . Otherwise I loses; the game
. Otherwise I loses; the game 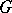 is determined if one of the players has a winning strategy. The Gale–Stewart theorem, which is easy but fundamental, asserts that all closed (or open) games are determined; it allows one to easily prove the second separation theorem and (cleverly used) that uncountable analytic sets contain perfect subsets. The difficult Martin theorem asserts that all Borel games are determined. On the other hand, one cannot prove in the usual Zermelo–Fraenkel system of axioms ZFC that analytic games are determined, and one is back to the problems unsolvable in ZFC alone (cf. [a9] and [a8] for most of the following results), the surrounding spaces being Polish:
is determined if one of the players has a winning strategy. The Gale–Stewart theorem, which is easy but fundamental, asserts that all closed (or open) games are determined; it allows one to easily prove the second separation theorem and (cleverly used) that uncountable analytic sets contain perfect subsets. The difficult Martin theorem asserts that all Borel games are determined. On the other hand, one cannot prove in the usual Zermelo–Fraenkel system of axioms ZFC that analytic games are determined, and one is back to the problems unsolvable in ZFC alone (cf. [a9] and [a8] for most of the following results), the surrounding spaces being Polish:
a) The statement "every countable P~11-set contains a perfect subset" , which is false in Gödel's constructible universe, is equivalent to "every S~31-set is measurable" and to "the constituents of a co-analytic non-Borel set are unbounded in Baire class" ; it follows from "all analytic games are determined" , which is equivalent to the "there is only one analytic non-Borel set, up to Borel isomorphism" and which follows from the existence of a measurable cardinal.
b) In Gödel's constructible universe there are 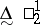 non-measurable sets or sets without the Baire property. However, every provably in ZFC
non-measurable sets or sets without the Baire property. However, every provably in ZFC 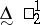 -set is measurable and has the Baire property.
-set is measurable and has the Baire property.
c) The axiom of projective determinacy, that all projective games are determined, which is equivalent to a "moderate" large cardinal axiom, implies that the classes 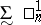 (respectively,
(respectively, 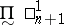 ) satisfy the separation property for odd
) satisfy the separation property for odd  , and the reduction and uniformization properties for even
, and the reduction and uniformization properties for even  . Moreover, all projective sets are measurable, have the Baire property and, if uncountable, contain a perfect set.
. Moreover, all projective sets are measurable, have the Baire property and, if uncountable, contain a perfect set.
The logicians who solved these historical problems also merged the classical theory and Kleene's recursion theory on 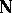 into a unified effective descriptive set theory (in the frame of Polish spaces). The impact on the classical theory has been varied. First new concepts and techniques have been introduced and theorems proved with no meaning in the classical theory, but which allow one to prove classical-type results for which no classical-type proofs existed; e.g., every co-analytic equivalence relation with uncountably many classes admits a perfect set of pairwise inequivalent elements. Secondly, as said above, it used and developed the game-theoretic techniques, from the classical and effective points of view. Finally, even if one reduces it by neglecting its effective aspects, it allowed one to discover powerful techniques in the realm of the classical theory:
into a unified effective descriptive set theory (in the frame of Polish spaces). The impact on the classical theory has been varied. First new concepts and techniques have been introduced and theorems proved with no meaning in the classical theory, but which allow one to prove classical-type results for which no classical-type proofs existed; e.g., every co-analytic equivalence relation with uncountably many classes admits a perfect set of pairwise inequivalent elements. Secondly, as said above, it used and developed the game-theoretic techniques, from the classical and effective points of view. Finally, even if one reduces it by neglecting its effective aspects, it allowed one to discover powerful techniques in the realm of the classical theory:
A) Because of Kleene's recursion theorem (cf. Recursion), universal sets are no longer useful only to get counter-examples, but have become fundamental objects. E.g., let 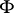 be a uniformly analytic operation from
be a uniformly analytic operation from 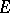 into
into  , i.e. a mapping from
, i.e. a mapping from  into
into 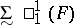 such that, for all
such that, for all 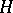 in
in  , the subset
, the subset 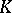 of
of 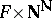 defined by
defined by 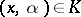
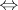
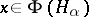 (where
(where 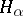 is the section of
is the section of 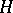 at
at 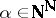 ) is analytic in
) is analytic in 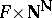 ; it follows from Kleene's recursion theorem (and classical ingredients) that
; it follows from Kleene's recursion theorem (and classical ingredients) that 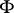 is increasing and satisfies the following generalization of the first separation theorem: If
is increasing and satisfies the following generalization of the first separation theorem: If  is analytic in
is analytic in 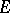 ,
, 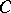 is co-analytic in
is co-analytic in 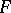 and
and 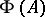 is a subset of
is a subset of 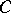 , there is a Borel set
, there is a Borel set 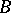 with
with 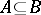 and
and 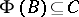 .
.
B) By a sensible abstract understanding of various classical results (Luzin–Sierpiński index, Luzin sieves, Novikov's comparison lemma ), the use of countable ordinals has become both more general and much easier, allowing one to reduce an important part of the classical heritage in the statement "every well-founded analytic relation on setswell-founded analytic relation has a countable length of an analytic relation on setslength" (a particular case of the Kunen–Martin theorem). Used together with A), it allows one to prove that if
), the use of countable ordinals has become both more general and much easier, allowing one to reduce an important part of the classical heritage in the statement "every well-founded analytic relation on setswell-founded analytic relation has a countable length of an analytic relation on setslength" (a particular case of the Kunen–Martin theorem). Used together with A), it allows one to prove that if 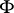 is a uniformly analytic derivation on
is a uniformly analytic derivation on 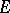 (i.e. a uniformly analytic operation from
(i.e. a uniformly analytic operation from 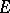 into
into 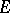 such that
such that 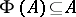 for each analytic set
for each analytic set  ), and if
), and if 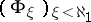 is the transfinite sequence of successive iterates, then i) for each analytic set
is the transfinite sequence of successive iterates, then i) for each analytic set 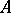 ,
, 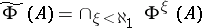 is analytic, and is the largest
is analytic, and is the largest 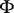 -invariant subset of
-invariant subset of 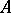 ; ii) the operation
; ii) the operation 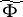 thus defined is uniformly analytic; and iii) if
thus defined is uniformly analytic; and iii) if 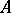 is analytic,
is analytic, 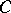 is co-analytic and contains
is co-analytic and contains 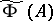 , then for some countable ordinal
, then for some countable ordinal 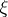 ,
, 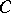 contains
contains 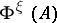 .
.
Descriptive set theory has important applications in any branch of analysis using measure theory (probability theory, optimization, game theory), particularly in theories rich in exceptional sets (potential theory, stochastic analysis, Hausdorff measure; harmonic analysis), but also in some others (Banach space theory). These applications rely on the following results about analytic sets in Polish spaces:
1) the stability properties of 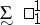 and the first separation theorem, together with the universal measurability, or the Baire property, of analytic sets;
and the first separation theorem, together with the universal measurability, or the Baire property, of analytic sets;
2) the Jankov–von Neumann theorem, which says that any analytic set in a product can be uniformized by the graph of a universally measurable function (which is much stronger than uniformization by a universally measurable graph);
3) the Choquet theorem, which says that every analytic set is universally capacitable (cf. Capacity), and, more generally, the fact that capacities and analytic sets are intimately linked;
4) finally, the Kunen–Martin theorem (for analytic sets).
Probably the two quite recent theorems on analytic operations quoted just above, which include the first separation theorem, the exterior approximation results in capacity theory and the so-called Kunen–Martin theorem, will be powerful tools in functional analysis.
References
| [a1] | W. Sierpiński, "Les ensembles projectifs et analytiques" , Gauthier-Villars (1950) |
| [a2] | N. Bourbaki, "Elements of mathematics. General topology" , 2 , Addison-Wesley (1966) (Translated from French) |
| [a3] | G. Choquet, "Outils topologiques et métriques de l'analyse mathématique" , Centre Docum. Univ. Paris (1969) (Rédigé par C. Mayer) |
| [a4] | J.P.R. Christensen, "Topology and Borel structure" , North-Holland (1977) |
| [a5] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , 1–3 , North-Holland (1978–1988) (Translated from French) |
| [a6] | J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) ((especially the article of D.A. Martin on Descriptive set theory)) |
| [a7] | A.S. Kechris, A. Louveau, "Descriptive set theory and the structure of sets of uniqueness" , Cambridge Univ. Press (1988) |
| [a8] | A. Louveau, "Ensembles analytiques et boréliens dans les espaces produits" Astérique , 78 (1980) |
| [a9] | Y.N. Moschovakis, "Descriptive set theory" , North-Holland (1980) |
| [a10] | C.A. Rogers, J.E. Jayne, C. Dellacherie, F. Tøpsoe, J. Hoffman-Jørgensen, D.A. Martin, A.S. Kechris, A.H. Stone, "Analytic sets" , Acad. Press (1980) |
| [a11] | R. Mansfield, G. Veitkamp, "Recursive aspects of descriptive set theory" , Oxford Univ. Press (1985) |
| [a12] | D.A. Martin, "Descriptive set theory: projective sets" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 783–815 |
| [a13] | T.J. Jech, "Set theory" , Acad. Press (1978) pp. Chapt. 7 (Translated from German) |
Descriptive set theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Descriptive_set_theory&oldid=11920