Descartes oval
A plane curve for which the distances  and
and  between any point
between any point  of the curve and two fixed points
of the curve and two fixed points  and
and  (the foci) are related by the non-homogeneous linear equation
(the foci) are related by the non-homogeneous linear equation
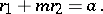 |
A Descartes oval may be defined by means of the homogeneous linear equation
 |
where  is the distance to the third focus
is the distance to the third focus  located on the straight line
located on the straight line 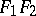 . In the general case, a Descartes oval consists of two closed curves, one enclosing the other (see Fig.). The equation of a Descartes oval in Cartesian coordinates is
. In the general case, a Descartes oval consists of two closed curves, one enclosing the other (see Fig.). The equation of a Descartes oval in Cartesian coordinates is
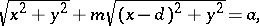 |
where 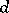 is the length of the segment
is the length of the segment 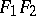 . If
. If 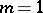 and
and 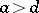 , the Descartes oval is an ellipse; if
, the Descartes oval is an ellipse; if 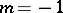 and
and 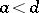 , it is a hyperbola; if
, it is a hyperbola; if 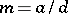 , it is a Pascal limaçon. First studied by R. Descartes in the context of problems of optics [1].
, it is a Pascal limaçon. First studied by R. Descartes in the context of problems of optics [1].

Figure: d031340a
References
| [1] | R. Descartes, "Géométrie" , Leyden (1637) |
| [2] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
A Descartes oval is also called a Cartesian oval, or simply a Cartesian.
The caustic of a circle with respect to a point light source in the plane of the circle is the evolute of a Descartes oval.
There are several ways in which a Cartesian oval can arise. One is as follows. Let 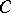 and
and 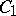 be two cones with axes parallel to the
be two cones with axes parallel to the  -axis and with circular intersections with the
-axis and with circular intersections with the 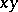 -plane. Then the vertical projection onto the
-plane. Then the vertical projection onto the 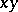 -plane of their intersection is a Cartesian oval. This is a result of A. Quetelet. Suppose the apexes of
-plane of their intersection is a Cartesian oval. This is a result of A. Quetelet. Suppose the apexes of 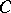 and
and 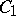 are at
are at  and
and 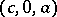 , respectively, and the intersections with the
, respectively, and the intersections with the 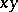 -plane are circles of radius 1 and
-plane are circles of radius 1 and 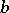 (see below). Then in the case
(see below). Then in the case 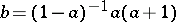 ,
,  the projection of the intersection is a cardioid.
the projection of the intersection is a cardioid.
In polar coordinates the equation for a Cartesian oval is  . Hence when
. Hence when 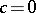 the equation becomes
the equation becomes 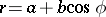 (plus
(plus 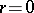 ) and one obtains the Pascal limaçon; when in addition
) and one obtains the Pascal limaçon; when in addition 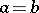 , the cardioid results, whose equation can also be written as
, the cardioid results, whose equation can also be written as  .
.
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
Descartes oval. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Descartes_oval&oldid=16712