Derived set
The collection 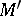 of all limit points of a set
of all limit points of a set 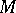 in a topological space (cf. Limit point of a set). A set
in a topological space (cf. Limit point of a set). A set 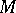 that coincides with its derived set is called perfect.
that coincides with its derived set is called perfect.
Comments
This process can be iterated.
In general one defines, for an ordinal number 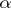 , the
, the 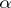 -th derived set of
-th derived set of 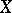 ,
, 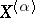 , as follows:
, as follows:  ,
, 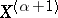 is the derived set of
is the derived set of 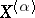 , and if
, and if 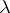 is a limit ordinal then
is a limit ordinal then 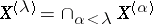 .
.
One then shows that there is a first ordinal number 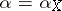 such that
such that 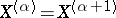 . If
. If 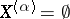 , then
, then 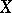 is called scattered; if
is called scattered; if 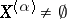 , then
, then 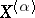 is called the perfect kernel of
is called the perfect kernel of 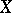 .
.
In this way one can prove the Cantor–Bendixson theorem: If 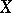 is a subspace of the real line, then
is a subspace of the real line, then 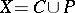 , with
, with 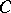 a countable set,
a countable set, 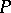 a perfect set and
a perfect set and 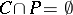 .
.
For this reason  is sometimes called the Cantor–Bendixson height of
is sometimes called the Cantor–Bendixson height of 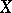 . Perfect spaces are sometimes called dense-in-itself.
. Perfect spaces are sometimes called dense-in-itself.
Derived set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derived_set&oldid=11226