Derived category
The notion of a derived category has been introduced by J.-L. Verdier in his 1963 notes [a7]. This facilitated a proof of a duality theorem of A. Grothendieck (cf. [a5]). Let 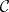 be an additive category equipped with an additive automorphism
be an additive category equipped with an additive automorphism 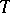 , called the translation functor. A triangle in
, called the translation functor. A triangle in 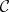 is a sextuple
is a sextuple 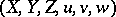 of objects
of objects 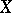 ,
, 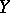 ,
, 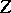 in
in 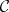 and morphism
and morphism 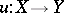 ,
, 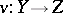 ,
, 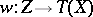 . One often uses
. One often uses
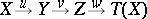 |
to denote such a triangle. It is obvious what it meant by a morphism of triangles. The category 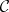 equipped with a family of triangles, the distinguished triangles, is called a triangulated category if the axioms TR1)–TR4) in [a7] are satisfied.
equipped with a family of triangles, the distinguished triangles, is called a triangulated category if the axioms TR1)–TR4) in [a7] are satisfied.
Writing briefly 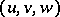 for a triangle
for a triangle 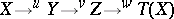 , these axioms are as follows.
, these axioms are as follows.
TR1) Each triangle isomorphic to a distinguished triangle is distinguished. For each morphism  there is a distinguished triangle
there is a distinguished triangle 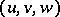 ;
; 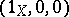 is distinguished.
is distinguished.
TR2) 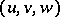 is distinguished if and only if
is distinguished if and only if 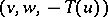 is distinguished.
is distinguished.
TR3) If 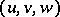 ,
, 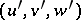 are distinguished and
are distinguished and 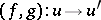 is a morphism, then there is an
is a morphism, then there is an 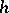 such that
such that 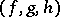 is a morphism of triangles.
is a morphism of triangles.
TR4) Let 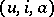 ,
, 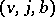 ,
, 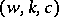 be three distinguished triangles with
be three distinguished triangles with 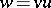 ,
, 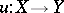 ,
, 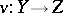 . Then there exists two morphisms
. Then there exists two morphisms 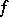 ,
, 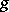 such that
such that 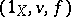 ,
, 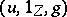 are morphisms of triangles and such that
are morphisms of triangles and such that 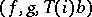 is a distinguished triangle.
is a distinguished triangle.
An additive functor between two triangulated categories is called a 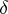 -functor (or exact functor) if it commutes with the translation functor and preserves distinguished triangles.
-functor (or exact functor) if it commutes with the translation functor and preserves distinguished triangles.
To get some feeling for these axioms and the terminology it is (perhaps) useful to keep the example below in mind: the category of complexes over an Abelian category (and algebraic mapping cones, the corresponding long exact sequences, and connecting homomorphisms of long exact sequences). One often writes a distinguished triangle 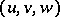 as
as
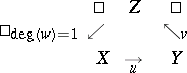 |
where 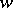 is thought of as a "morphism of degree 1" from
is thought of as a "morphism of degree 1" from  (which, by definition, is the same thing as a morphism
(which, by definition, is the same thing as a morphism 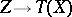 ). Whence the terminology "triangulated category" . Writing
). Whence the terminology "triangulated category" . Writing 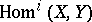 for the group of morphisms
for the group of morphisms 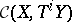 one finds straightforwardly from TR1)–TR3) for each distinguished triangle and object
one finds straightforwardly from TR1)–TR3) for each distinguished triangle and object 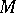 of
of 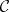 long exact sequences of groups
long exact sequences of groups
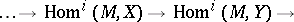 |
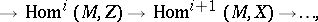 |
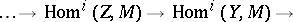 |
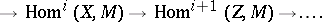 |
The next step, still inspired by cohomology and complexes, is to "localize suitably" , i.e. "to find a categorical setting in which morphisms which induce isomorphisms in cohomology can be inverted and thus become isomorphisms" .
Let 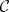 be a triangulated category. A collection
be a triangulated category. A collection 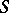 of morphism s in
of morphism s in 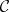 is called a multiplicative system if it satisfies properties (FR1)–(FR5) (given in [a7]).
is called a multiplicative system if it satisfies properties (FR1)–(FR5) (given in [a7]).
(FR1) If 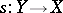 and
and 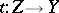 are in
are in 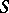 , then so is
, then so is 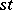 . All identity morphisms are in
. All identity morphisms are in 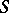 .
.
(FR2) If 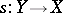 is in
is in 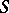 and
and 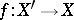 , then there are an
, then there are an 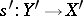 in
in 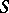 and a
and a 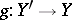 such that
such that 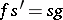 , and (symmetrically) if
, and (symmetrically) if 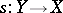 is in
is in 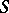 and
and 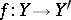 , then there are an
, then there are an 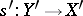 in
in 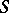 and a
and a 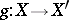 such that
such that 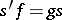 .
.
(FR3) For all 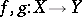 there are
there are 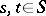 such that
such that 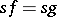 ,
,  .
.
(FR4) If 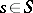 , then also
, then also 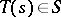 .
.
(FR5) If 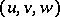 and
and 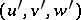 are two distinguished triangles and
are two distinguished triangles and 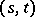 is a morphism from
is a morphism from  to
to 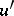 with
with 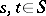 , then there is an
, then there is an 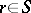 such that
such that 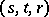 is a morphism of distinguished triangles.
is a morphism of distinguished triangles.
Axioms (FR1) and (FR2), and to a lesser extent (FR3), are "general" in the setting of categories of fractions (cf. (the comments to) Localization in categories). The other two are special for this particular setting of triangulated categories.
The localization of 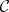 with respect to
with respect to 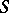 is a category
is a category 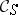 together with the canonical functor
together with the canonical functor 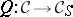 such that the pair
such that the pair 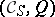 has the universal property: Any functor
has the universal property: Any functor 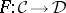 such that
such that 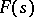 is an isomorphism for all
is an isomorphism for all 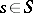 factors uniquely through
factors uniquely through 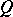 .
.
Such a pair exists and, moreover, 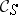 carries a unique structure of a triangulated category such that
carries a unique structure of a triangulated category such that 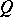 is exact. Note that the objects of
is exact. Note that the objects of 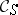 are the objects of
are the objects of 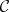 and that a morphism from
and that a morphism from 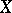 to
to 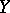 in
in 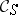 may be represented by a diagram
may be represented by a diagram 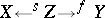 of morphisms in
of morphisms in 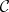 such that
such that 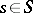 .
.
Let 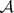 be an Abelian category. Denote by
be an Abelian category. Denote by 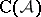 the additive category of complexes of
the additive category of complexes of 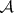 . The translation functor
. The translation functor 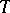 is defined by
is defined by 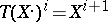 ,
, 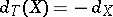 , and one often writes
, and one often writes 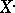 instead of
instead of 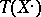 [a1]. Denoted by
[a1]. Denoted by 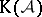 the additive category whose objects are the objects of
the additive category whose objects are the objects of 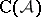 and whose morphisms are homotopy equivalence classes of morphisms in
and whose morphisms are homotopy equivalence classes of morphisms in 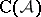 . Call a triangle distinguished if it is isomorphic to a triangle of the form
. Call a triangle distinguished if it is isomorphic to a triangle of the form 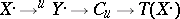 . Here
. Here 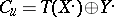 denotes the maping cone (cf. Mapping-cone construction) of
denotes the maping cone (cf. Mapping-cone construction) of  . Similarly one defines
. Similarly one defines 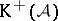 (respectively,
(respectively, 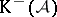 , respectively,
, respectively, 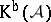 ), the category of bounded below (respectively, bounded above, respectively, bounded) complexes of
), the category of bounded below (respectively, bounded above, respectively, bounded) complexes of 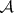 . A complex
. A complex 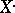 is bounded above if
is bounded above if 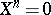 for
for  large enough, etc.
large enough, etc.
Let 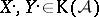 . A morphism
. A morphism 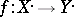 is called a quasi-isomorphism if it induces an isomorphism on cohomology. Let
is called a quasi-isomorphism if it induces an isomorphism on cohomology. Let 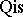 be the collection of all quasi-isomorphisms. The localized category (cf. Localization in categories)
be the collection of all quasi-isomorphisms. The localized category (cf. Localization in categories) 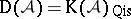 is called the derived category of
is called the derived category of 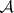 . Similarly one defines
. Similarly one defines 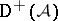 (respectively,
(respectively, 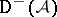 , respectively,
, respectively, 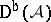 ). Every short exact sequence gives rise to a distinguished triangle in
). Every short exact sequence gives rise to a distinguished triangle in 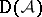 .
.
Assume that 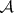 has enough injectives (cf. Injective object). Denote by
has enough injectives (cf. Injective object). Denote by 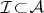 the collection of injective objects in
the collection of injective objects in 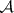 and let
and let 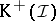 be the triangulated subcategory of
be the triangulated subcategory of 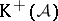 consisting of bounded below complexes of injective objects in
consisting of bounded below complexes of injective objects in 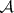 . The canonical functor
. The canonical functor 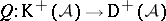 induces an equivalence of categories
induces an equivalence of categories 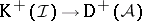 . A similar discussion applies to
. A similar discussion applies to 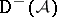 in case
in case 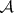 has enough projectives (cf. Projective object of a category).
has enough projectives (cf. Projective object of a category).
Finally, let 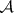 be an Abelian category and let
be an Abelian category and let 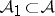 be a thick Abelian subcategory. Define
be a thick Abelian subcategory. Define 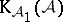 as the full triangulated subcategory of
as the full triangulated subcategory of 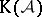 consisting of the complexes whose cohomology objects are in
consisting of the complexes whose cohomology objects are in 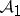 , and put
, and put 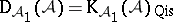 . This is the full subcategory of
. This is the full subcategory of 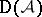 consisting of those complexes whose cohomology objects are in
consisting of those complexes whose cohomology objects are in 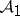 .
.
The derived functor.
Let 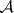 and
and 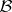 be Abelian categories. Let
be Abelian categories. Let 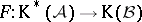 be a
be a 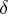 -functor (where
-functor (where  is
is 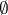 ,
, 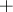 ,
,  , or b). One says that the right derived functor
, or b). One says that the right derived functor 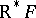 (respectively, left derived functor
(respectively, left derived functor 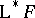 ) of
) of 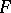 exists if the functor
exists if the functor 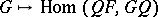 (respectively,
(respectively, 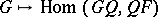 ) from the category of
) from the category of  -functors
-functors  to the category of sets is representable (cf. Representable functor). In that case
to the category of sets is representable (cf. Representable functor). In that case 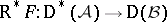 (respectively,
(respectively, 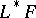 ) is, by definition, a representative. For every
) is, by definition, a representative. For every 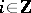 one puts
one puts  (respectively,
(respectively, 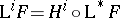 ).
).
Concerning existence one has the following. Suppose 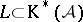 is a triangulated subcategory such that: 1) every object of
is a triangulated subcategory such that: 1) every object of 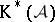 admits a quasi-isomorphism into (respectively, from) an object of
admits a quasi-isomorphism into (respectively, from) an object of 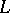 ; and 2) for every acyclic object
; and 2) for every acyclic object 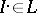 ,
, 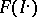 is acyclic. (An acyclic complex
is acyclic. (An acyclic complex 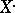 is one whose cohomology is zero.) Then the right derived functor
is one whose cohomology is zero.) Then the right derived functor 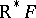 (respectively, left derived functor
(respectively, left derived functor 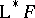 ) exists and for every object
) exists and for every object 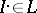 one has
one has 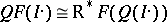 (respectively,
(respectively, 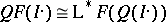 ).
).
Let 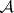 and
and 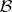 be Abelian categories and let
be Abelian categories and let 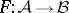 be an additive left exact (respectively, right exact) functor (cf. Exact functor). Suppose that
be an additive left exact (respectively, right exact) functor (cf. Exact functor). Suppose that 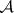 has enough injective (respectively, projective) objects. Then
has enough injective (respectively, projective) objects. Then 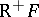 (respectively,
(respectively, 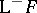 ) exists. The functor
) exists. The functor 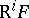 (respectively,
(respectively, 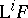 ) coincides with the usual
) coincides with the usual 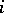 -th right (respectively, left) derived functor of
-th right (respectively, left) derived functor of 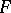 .
.
The most important property is the following. Let 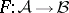 ,
, 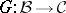 be additive left exact functors between Abelian categories. Assume that
be additive left exact functors between Abelian categories. Assume that 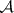 and
and 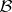 have enough injective objects. Assume
have enough injective objects. Assume 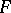 sends injective objects into
sends injective objects into 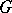 -acyclic objects. Then
-acyclic objects. Then 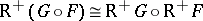 . A similar statement holds for left derived functors. See also Derived functor.
. A similar statement holds for left derived functors. See also Derived functor.
Verdier duality.
The concept of derived categories is very well suited to state and prove a result on duality by Verdier (cf. [a8]). For related topics such as Alexander duality and Poincaré duality see also [a6]. Let 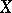 and
and 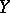 be topological spaces and let
be topological spaces and let 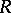 be a Noetherian ring. Suppose that
be a Noetherian ring. Suppose that 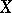 and
and 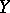 are locally compact and of finite dimension. Let
are locally compact and of finite dimension. Let 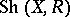 be the Abelian category of sheaves of
be the Abelian category of sheaves of 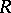 -modules. This category has enough injective objects. Denote by
-modules. This category has enough injective objects. Denote by 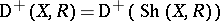 the derived category. Consider a continuous mapping
the derived category. Consider a continuous mapping 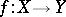 and let
and let 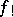 be the functor direct image with proper support. This is an additive left exact functor.
be the functor direct image with proper support. This is an additive left exact functor.
Verdier duality. There exists an additive functor 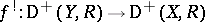 and a natural isomorphism
and a natural isomorphism 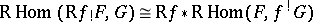 , for all
, for all 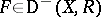 ,
, 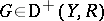 .
.
Suppose that 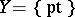 and put
and put 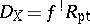 . This is called the dualizing sheaf on
. This is called the dualizing sheaf on 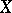 . For any object
. For any object 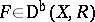 the Verdier dual of
the Verdier dual of 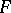 is
is 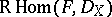 .
.
References
| [a1] | A.A. Beilinson, J. Bernstein, P. Deligne, "Faisceaux pervers" Astérisque. Analyse et topologie sur les espaces singuliers (I) , 100 (1982) |
| [a2] | A. Borel, et al., "Intersection cohomology" , Birkhäuser (1984) |
| [a3] | P. Deligne, "Cohomology à supports propres" , Sem. Geom. Alg. 4. Exp. 17 , Lect. notes in math. , 305 , Springer (1973) pp. 82–115 |
| [a4] | P.-P. Grivel, "Catégories derivées et foncteurs derivés" A. Borel (ed.) et al. (ed.) , Algebraic  -modules , Acad. Press (1987) pp. 1–108 -modules , Acad. Press (1987) pp. 1–108 |
| [a5] | R. Hartshorne, "Residues and duality" , Springer (1966) |
| [a6] | B. Iversen, "Cohomology of sheaves" , Springer (1986) |
| [a7] | J.-L. Verdier, "Categories derivées, Etat 0" , Sem. Geom. Alg. 4 1/2. Cohomologie etale , Lect. notes in math. , 569 , Springer (1977) pp. 262–311 |
| [a8] | J.-L. Verdier, "Dualité dans la cohomologie des espaces localement compacts" , Sem. Bourbaki. Exp 300 (1965–1966) |
Derived category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derived_category&oldid=16285