Derivative
One of the basic concepts in mathematical analysis. Suppose that a real-valued function  of a real variable
of a real variable  is defined in a neighbourhood of a point
is defined in a neighbourhood of a point  and that there exists a finite or infinite limit
and that there exists a finite or infinite limit
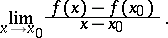 | (*) |
This limit is called the derivative of the function  at the point
at the point  . If one sets
. If one sets  ,
,
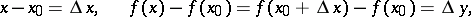 |
then the limit (*) can be written as:
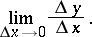 |
Also the notations 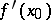 ,
,  ,
, 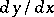 ,
,  , and some others are used to denote this limit.
, and some others are used to denote this limit.
The operation of computing the derivative is called differentiation. If the derivative 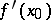 is finite,
is finite, 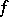 is said to be differentiable at the point
is said to be differentiable at the point 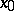 . A function differentiable at every point of a set is said to be differentiable on that set. A differentiable function is always continuous. However, there are continuous functions that have no derivative at any point of a given interval (see Non-differentiable function).
. A function differentiable at every point of a set is said to be differentiable on that set. A differentiable function is always continuous. However, there are continuous functions that have no derivative at any point of a given interval (see Non-differentiable function).
Let a function 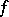 be differentiable in an interval. Its derivative
be differentiable in an interval. Its derivative 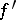 may turn out to be a discontinuous function. However, according to Baire's classification (see Baire classes) it is always a function of the first class and has the Darboux property: If it takes two values, it takes every intermediate value as well.
may turn out to be a discontinuous function. However, according to Baire's classification (see Baire classes) it is always a function of the first class and has the Darboux property: If it takes two values, it takes every intermediate value as well.
A generalization of the concept of the derivative is the concept of a derivative over a set. Suppose that a real-valued function 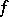 is defined on a set
is defined on a set 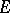 of real numbers, that
of real numbers, that 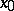 is a limit point of
is a limit point of 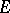 , that
, that 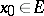 , and that there exists a finite or infinite limit
, and that there exists a finite or infinite limit
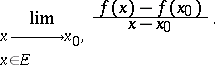 |
This limit is called the derivative of 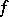 over the set
over the set 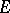 at the point
at the point 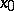 and is denoted by the symbol
and is denoted by the symbol 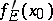 . The derivative of a function over a set is a generalization of the concept of a derivative. Variations of the generalization are the concept of a one-sided derivative, a Dini derivative, and an approximate derivative.
. The derivative of a function over a set is a generalization of the concept of a derivative. Variations of the generalization are the concept of a one-sided derivative, a Dini derivative, and an approximate derivative.
The above definition of the derivative (and its generalizations), as well as simple properties of it, extend almost without change to complex-valued and vector-valued functions of a real or complex variable. Moreover, there exists a concept of a derivative of a scalar-valued point function in a Euclidean space 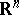 (see Gradient), and of a derivative of a set function with respect to a measure (in particular, with respect to area, volume, etc.). The concept of a derivative is extended to vector-valued point functions in an abstract space (see Differentiation of a mapping).
(see Gradient), and of a derivative of a set function with respect to a measure (in particular, with respect to area, volume, etc.). The concept of a derivative is extended to vector-valued point functions in an abstract space (see Differentiation of a mapping).
For a geometric and mechanical interpretation of the derivative, the simplest rules of differentiation, higher derivatives, partial derivatives, and also for references see Differential calculus.
Comments
G. Choquet has proved that a function 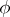 on
on 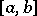 is of the first Baire class and has the Darboux property (if and) only if there exists a differentiable function
is of the first Baire class and has the Darboux property (if and) only if there exists a differentiable function 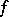 on
on 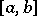 and a homeomorphism
and a homeomorphism 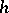 of
of 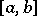 such that
such that 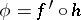 . See [a1] for details and references.
. See [a1] for details and references.
References
| [a1] | G. Choquet, "Outils topologiques et métriques de l'analyse mathématique" , Centre Docum. Univ. Paris (1969) (Rédigé par C. Mayer) MR0262426 |
Derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derivative&oldid=39010