Derivation rule
A method for generating objects, called conclusions of the derivation rule, from a set of objects called the premises of the rule; the formulation of a derivation rule plays a determining role in describing calculi (cf. Calculus) (a given derivation rule is often meaningful only in the context of a specific calculus). For calculi with semantics (in particular, in most logico-mathematical calculi, cf. Logico-mathematical calculus) a derivation rule preserves truth, i.e. true premises permit true conclusions only; the most prominent example of such a derivation rule is the rule of modus ponens. In most calculi being studied, a derivation rule has only a finite number of premises (the most important exception is the Carnap rule). As a rule, the number of premises of a given derivation rule remains unchanged in all its applications. The number of possible applications of a given rule, however, is in principle unlimited.
The methods of formulation of a derivation rule are extremely varied; they depend on the language of the calculus and may include variables of different types. The great majority of derivation rules may be generated according to the following general scheme: After an alphabet  not containing the letter
not containing the letter  and a natural number
and a natural number  have been selected, a derivation rule with
have been selected, a derivation rule with  -premises is defined as some algorithm
-premises is defined as some algorithm  over the alphabet
over the alphabet  . If
. If  is applicable to the word
is applicable to the word  , where
, where 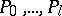 are words over
are words over 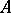 , while the symbol
, while the symbol  serves as the comma, then
serves as the comma, then 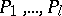 are regarded as the premises, while
are regarded as the premises, while 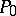 is regarded as the conclusion of some specific application of the derivation rule. A special case of such derivation rules are derivation rules without premises (or axiom schemes, cf. Axiom scheme). In any calculus containing only such rules, the set of deducible words is countable. A derivation rule often satisfies a more rigorous requirement as well: It is possible to tell, with the aid of algorithms, whether
is regarded as the conclusion of some specific application of the derivation rule. A special case of such derivation rules are derivation rules without premises (or axiom schemes, cf. Axiom scheme). In any calculus containing only such rules, the set of deducible words is countable. A derivation rule often satisfies a more rigorous requirement as well: It is possible to tell, with the aid of algorithms, whether 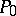 is deducible from
is deducible from 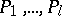 by one application of the rule.
by one application of the rule.
Comments
Often, instead of "derivation rule" one simply uses the word "rulerule" . Modus ponens, e.g., is sometimes referred to as the rule of detachment.
References
| [a1] | A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974) |
| [a2] | J.B. Rosser, "Logic for mathematicians" , McGraw-Hill (1953) |
Derivation rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derivation_rule&oldid=16445