Derivation in a ring
A mapping  of a ring
of a ring 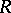 into itself which is an endomorphism of the additive group of
into itself which is an endomorphism of the additive group of  and satisfies the relation
and satisfies the relation
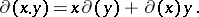 |
Let 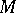 be a left
be a left 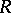 -module. A derivation in
-module. A derivation in 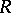 with values in
with values in  is a homomorphism of the respective additive groups which satisfies the condition
is a homomorphism of the respective additive groups which satisfies the condition
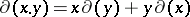 |
for all 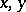 from
from 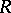 . For any element
. For any element  from the centre
from the centre 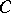 of
of 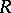 , the mapping
, the mapping  , where
, where 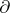 is a derivation, is a derivation. The sum of two derivations is also a derivation. This defines the structure of a
is a derivation, is a derivation. The sum of two derivations is also a derivation. This defines the structure of a 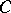 -module on the set of all derivations in
-module on the set of all derivations in 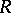 with values in
with values in 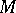 , denoted by
, denoted by 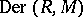 . If
. If 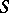 is a subring in
is a subring in 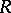 , a derivation
, a derivation 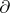 such that
such that 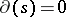 for all
for all  is known as an
is known as an 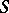 -derivation. The set of all
-derivation. The set of all 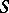 -derivations forms a submodule in
-derivations forms a submodule in 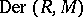 , denoted by
, denoted by 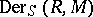 . The operation
. The operation
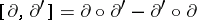 |
defines the structure of a Lie 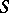 -algebra on the
-algebra on the 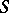 -module
-module 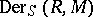 . If
. If 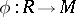 is a homomorphism of
is a homomorphism of 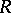 -modules, then the composition
-modules, then the composition 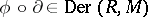 for any
for any 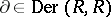 .
.
Let 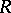 be a ring of polynomials
be a ring of polynomials 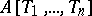 with coefficients in a commutative ring
with coefficients in a commutative ring  . The mapping
. The mapping
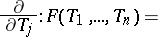 |
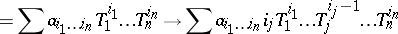 |
is an 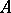 -derivation in
-derivation in  , and the
, and the 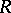 -module
-module  is a free module with basis
is a free module with basis 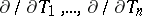 .
.
For any element  of an associative ring (or a Lie algebra)
of an associative ring (or a Lie algebra) 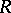 the mapping
the mapping 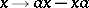 (or
(or 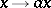 ) is a derivation in
) is a derivation in 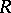 , known as an inner derivation. Derivations which are not inner are known as outer.
, known as an inner derivation. Derivations which are not inner are known as outer.
If 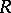 is a subring of a ring
is a subring of a ring 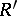 and if
and if 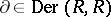 , one says that
, one says that 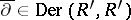 is an extension of
is an extension of 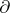 if the restriction of
if the restriction of 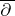 to
to 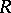 coincides with
coincides with 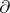 . If
. If 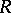 is a commutative integral ring and
is a commutative integral ring and 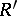 is its field of fractions, and also if
is its field of fractions, and also if  is a separable algebraic extension of the field
is a separable algebraic extension of the field 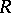 or if
or if 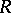 is a Lie algebra over a field
is a Lie algebra over a field 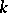 and
and  is its enveloping algebra, there exists a unique extension of any derivation
is its enveloping algebra, there exists a unique extension of any derivation 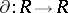 to
to 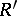 .
.
There is a close connection between derivations and ring isomorphisms. Thus, if 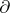 is a nilpotent derivation, that is, for some
is a nilpotent derivation, that is, for some  ,
,  , and
, and 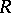 is an algebra over a field of characteristic zero, the mapping
is an algebra over a field of characteristic zero, the mapping
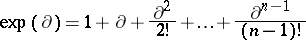 |
is an automorphism of the 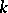 -algebra
-algebra 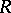 . If
. If 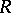 is a local commutative ring with maximal ideal
is a local commutative ring with maximal ideal 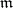 , there is a bijection between the set of derivations
, there is a bijection between the set of derivations 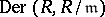 and the set of automorphisms of the ring
and the set of automorphisms of the ring 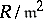 which induces the identity automorphism of the residue field
which induces the identity automorphism of the residue field 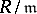 . Derivations of non-separable field extensions play the role of elements of the Galois group of separable extensions in the Galois theory of such extensions [4].
. Derivations of non-separable field extensions play the role of elements of the Galois group of separable extensions in the Galois theory of such extensions [4].
References
| [1] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Addison-Wesley (1973) (Translated from French) |
| [2] | N. Jacobson, "The theory of rings" , Amer. Math. Soc. (1943) |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [4] | J. Mordeson, B. Vinograde, "Strucuture of arbitrary purely inseparable extension fields" , Springer (1970) |
Comments
The 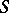 -derivations in
-derivations in 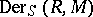 are precisely the
are precisely the 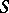 -linear mappings from
-linear mappings from 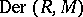 . If
. If 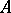 is an
is an 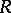 -algebra, then a derivation in
-algebra, then a derivation in 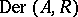 is a crossed homomorphism
is a crossed homomorphism 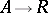 or, equivalently, a Hochschild
or, equivalently, a Hochschild 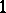 -cocycle.
-cocycle.
If the Lie algebra 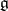 is semi-simple, all derivations
is semi-simple, all derivations 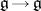 are inner, i.e. in that case
are inner, i.e. in that case 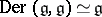 .
.
Let 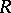 be any algebra (or ring), not necessarily commutative or associative. The algebra is said to be Lie admissible if the associated algebra
be any algebra (or ring), not necessarily commutative or associative. The algebra is said to be Lie admissible if the associated algebra 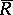 with multiplication
with multiplication 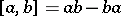 is a Lie algebra. Associative algebras and Lie algebras are Lie admissible, but there are also other examples. These algebras were introduced by A.A. Albert in 1948.
is a Lie algebra. Associative algebras and Lie algebras are Lie admissible, but there are also other examples. These algebras were introduced by A.A. Albert in 1948.
A ring  together with a derivation
together with a derivation 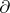 is a differential ring, cf. also Differential algebra and Differential field.
is a differential ring, cf. also Differential algebra and Differential field.
Derivation in a ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derivation_in_a_ring&oldid=17037