Derivation, logical
A formal derivation in a calculus which involves logical rules, and the main outcome of which is a formula interpreted as a proposition; see Logical calculus; Logico-mathematical calculus. Since such calculi are usually endowed with a semantics, a logical derivation is sometimes understood to mean a meaningful statement permitting to pass from formulated axioms and hypotheses (assumptions) to new propositions which are a logical consequence of the starting ones.
If the axioms and the rules of logical transitions are given (cf. Derivation rule), one says that the sequence of formulas is a derivation (of its last term  ) from the hypotheses
) from the hypotheses  (
( ), if each term of the sequence is an axiom, is one of the hypotheses or else may be obtained from the preceding formulas in accordance with one of the rules. This is written as
), if each term of the sequence is an axiom, is one of the hypotheses or else may be obtained from the preceding formulas in accordance with one of the rules. This is written as  . Formula
. Formula 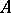 is then called derivable from
is then called derivable from  . If
. If  , the notation
, the notation  means that
means that  is derivable in the relevant calculus without any assumptions; the notation
is derivable in the relevant calculus without any assumptions; the notation 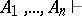 , which means that "the assumptions A1…An lead to a contradiction" , is also employed (in most systems being studied
, which means that "the assumptions A1…An lead to a contradiction" , is also employed (in most systems being studied 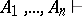 means that any formula at all may be deduced from these hypotheses). For instance, in a calculus containing the axiom
means that any formula at all may be deduced from these hypotheses). For instance, in a calculus containing the axiom 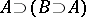 and the rule of modus ponens, the sequence
and the rule of modus ponens, the sequence 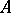 ,
, 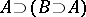 ,
, 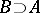 , is a derivation of
, is a derivation of 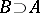 from
from 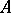 (i.e.
(i.e. 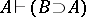 ). The following are properties of logical derivability:
). The following are properties of logical derivability: 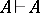 ; if
; if 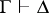 , then
, then 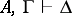 ; if
; if 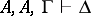 , then
, then 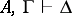 ; if
; if 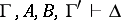 , then
, then 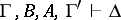 ; if
; if  and
and 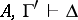 , then
, then 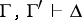 (here
(here 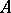 and
and 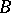 are formulas,
are formulas, 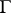 and
and 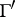 are lists of formulas and
are lists of formulas and 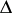 is a formula or the empty word). These formulas make a substantial transformation of the list of hypotheses possible and, in conjunction with the rules of introduction and elimination of logical symbols (cf. Derived rule; Deducible rule), render systems with the symbol
is a formula or the empty word). These formulas make a substantial transformation of the list of hypotheses possible and, in conjunction with the rules of introduction and elimination of logical symbols (cf. Derived rule; Deducible rule), render systems with the symbol 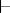 much like a Gentzen formal system. In calculi based on classical logic, a characteristic property is
much like a Gentzen formal system. In calculi based on classical logic, a characteristic property is 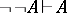 . In intuitionistic logic (constructive logic) it is possible to demonstrate, under certain assumptions on
. In intuitionistic logic (constructive logic) it is possible to demonstrate, under certain assumptions on  , the principles of Brouwer's concept of derivability: 1) if
, the principles of Brouwer's concept of derivability: 1) if 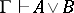 , then either
, then either  or
or 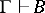 ; and 2) if
; and 2) if  , then, for some term
, then, for some term 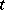 ,
, 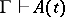 (these assumptions are invariably met for the empty
(these assumptions are invariably met for the empty 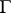 ). Possibilities of discarding certain assumptions, including transitions to conclusions without any hypotheses, are governed by a deduction theorem.
). Possibilities of discarding certain assumptions, including transitions to conclusions without any hypotheses, are governed by a deduction theorem.
The formulation of the concept of a derivation (and of the systems in terms of which this concept is meaningful) heralded the advent of modern mathematical logic. The modern, more rigorous interpretation of the axiomatic method, in which not only axioms but also logical tools are formalized, made it possible to give a mathematical definition of the concept of a proof and of studying proofs by mathematical methods (cf. Proof theory). The concept of a formal derivation proved to be a good approximation to the concept of a mathematical proof (cf. Gödel completeness theorem; Gödel incompleteness theorem). The artefact formalization of logical deducibility subsequently came nearer to the real methods of meaningful mathematical reasoning (cf. Natural logical deduction).
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
| [2] | , Mathematical theory of logical deduction , Moscow (1967) (In Russian; translated from English) (Collection of translations) |
Derivation, logical. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derivation,_logical&oldid=11644