Derangement

derangement

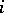A permutation of elements in which the element cannot occupy the 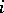-th position, 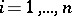. The problem of calculating the number 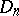of derangements is known as the "problème des rencontresproblème des rencontres" . The following formula holds:

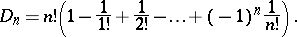Derangements are a special case of permutations satisfying a specific restriction on the position of the permuted elements. For example, the "problème des ménagesproblème des ménages" consists in calculating the number 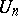of permutations conflicting with the two permutations 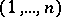and 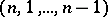. (Two permutations of elements are called conflicting if the 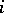-th element occupies different positions in each of them for all ). The number 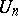is given by the formula:

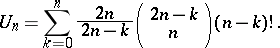The number 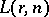of Latin squares (cf. Latin square) of size 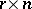for can be calculated in terms of 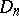and by the formulas

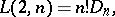References

[1]	H.J. Ryser, "Combinatorial mathematics" , Carus Math. Monogr. , 14 , Wiley & Math. Assoc. Amer. (1963)
[2]	J. Riordan, "An introduction to combinatorial mathematics" , Wiley (1958)