Depth of a module
One of the cohomological characteristics of a module over a commutative ring. Let  be a Noetherian ring, let
be a Noetherian ring, let  be an ideal in it and let
be an ideal in it and let  be an
be an  -module of finite type. Then the
-module of finite type. Then the  -depth of the module
-depth of the module  is the least integer
is the least integer  for which
for which
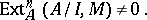 |
The depth of a module is denoted by 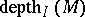 or by
or by  . A different definition can be given in terms of an
. A different definition can be given in terms of an 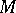 -regular sequence, i.e. a sequence of elements
-regular sequence, i.e. a sequence of elements  of
of  such that
such that 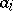 is not a zero divisor in the module
is not a zero divisor in the module
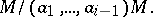 |
The  -depth of
-depth of 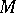 is equal to the length of the largest
is equal to the length of the largest  -regular sequence consisting of elements of
-regular sequence consisting of elements of 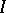 . The maximal ideal is usually taken for
. The maximal ideal is usually taken for 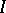 in the case of a local ring
in the case of a local ring 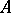 . The following formula is valid:
. The following formula is valid:
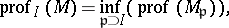 |
where  denotes a prime ideal in
denotes a prime ideal in  , while
, while  is considered as a module over the local ring
is considered as a module over the local ring  .
.
The concept of the depth of a module was introduced in [1] under the name of homological codimension. If the projective dimension 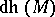 of a module
of a module  over a local ring
over a local ring 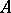 is finite, then
is finite, then
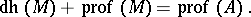 |
In general  is not larger than the dimension of
is not larger than the dimension of  .
.
The depth of a module is one of the basic tools in the study of modules. Thus, Cohen–Macaulay modules and rings (cf. Cohen–Macaulay ring) have been defined in terms of the depth of modules. The Serre criterion (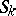 ) for an
) for an 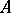 -module
-module 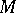 :
:
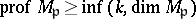 |
for all prime ideals  in
in  , often proves to be useful. Finally, the depth of modules is closely connected with local cohomology modules: The statement
, often proves to be useful. Finally, the depth of modules is closely connected with local cohomology modules: The statement
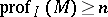 |
is equivalent to saying that the local cohomology modules 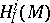 vanish if
vanish if 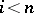 .
.
References
| [1] | M. Auslander, D.A. Buchsbaum, "Homological dimension in Noetherian rings" Proc. Nat. Acad. Sci. USA , 42 (1956) pp. 36–38 |
| [2] | J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1965) |
| [3] | A. Grothendieck, "Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux" , SGA 2 , IHES (1965) |
Depth of a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Depth_of_a_module&oldid=17353