Denumerant
From Encyclopedia of Mathematics
The number 
of partitions of an integer 
into parts equal to 
, i.e. the number of solutions in non-negative integers of the equation
 |
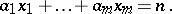The generating function of the denumerants is
 |
 |
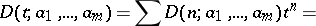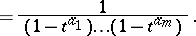The simplest method of computing a denumerant is by Euler's recurrence relation:
 |
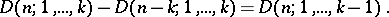Explicit formulas for certain denumerants may be obtained from the following theorem: If 
is the least common multiple of the numbers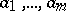 
, then the denumerant
 |
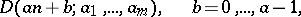is a polynomial of degree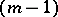 
with respect to 
.
References
| [1] | J. Riordan, "An introduction to combinational analysis" , Wiley (1958) |
How to Cite This Entry:
Denumerant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Denumerant&oldid=16405
Denumerant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Denumerant&oldid=16405
This article was adapted from an original article by V.E. Tarakanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article