Density of a sequence
A concept in general additive number theory, in which one studies addition laws for sequences of general form. The density of a sequence is a measure of what part of the sequence of all natural numbers belongs to a given sequence  of integers
of integers 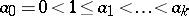 . By the density of a sequence
. By the density of a sequence 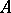 one means the density
one means the density 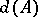 (introduced in 1930 by L.G. Shnirel'man) of
(introduced in 1930 by L.G. Shnirel'man) of  , namely
, namely
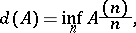 |
where
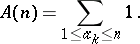 |
The density 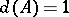 if and only if
if and only if  coincides with the set
coincides with the set 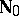 of all non-negative integers. Let
of all non-negative integers. Let  be the arithmetic sum of two sequences
be the arithmetic sum of two sequences  and
and  , i.e. the set
, i.e. the set 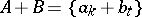 where the numbers
where the numbers  are taken without repetition. If
are taken without repetition. If 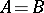 , one puts
, one puts  , and similarly
, and similarly 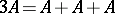 , etc. If
, etc. If 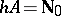 , then
, then  is called a basis of order
is called a basis of order  . On examining the structures of sets obtained by summing sequences determined only by their densities, one uses the following theorems on the density of the sum of two sequences:
. On examining the structures of sets obtained by summing sequences determined only by their densities, one uses the following theorems on the density of the sum of two sequences:
 |
(Shnirel'man's inequality) and the stronger inequality
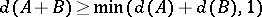 |
(the Mann–Dyson inequality).
Shnirel'man's inequality implies that any sequence of positive density is a basis of finite order. This can be used in additive problems, in which one frequently sums sequences of zero density by the preliminary construction of new sequences with positive density from the given ones. For example, it has been shown by sieve methods that the sequence  , where
, where  runs through the prime numbers, has positive density. Shnirel'man's theorem follows from this: There exists an integer
runs through the prime numbers, has positive density. Shnirel'man's theorem follows from this: There exists an integer  such that any natural number is the sum of at most
such that any natural number is the sum of at most 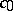 prime numbers. This theorem gives a solution to the so-called weak Goldbach problem (see also Additive number theory).
prime numbers. This theorem gives a solution to the so-called weak Goldbach problem (see also Additive number theory).
A variant of this concept of density is that of asymptotic density, a particular case of this being the natural density. The concept of density is also extended to numerical sequences differing from the natural sequence, for example to the sequence of integers in algebraic number fields. As a result it is possible to examine bases in algebraic fields.
References
| [1] | A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian) |
| [2] | H.H. Ostmann, "Additive Zahlentheorie" , Springer (1956) |
Density of a sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_of_a_sequence&oldid=11233