Density method
One of the methods in analytic number theory based on the study of statistics of the distribution of the zeros of the Riemann zeta-function
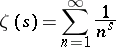 |
and Dirichlet  -functions
-functions
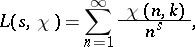 |
where  and
and  is a character modulo
is a character modulo  . Many number-theoretic problems obtain their final solution on the assumption that all the zeros
. Many number-theoretic problems obtain their final solution on the assumption that all the zeros  of the functions
of the functions  and
and 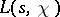 in the strip
in the strip 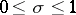 ,
,  lie on the straight line
lie on the straight line 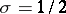 . However, in some cases, sufficiently strong results are obtained if one can show that the zeros of these functions with abscissas
. However, in some cases, sufficiently strong results are obtained if one can show that the zeros of these functions with abscissas 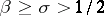 , if they exist, constitute a set that becomes more sparse as
, if they exist, constitute a set that becomes more sparse as  . There are numerous theorems that give upper bounds for the number
. There are numerous theorems that give upper bounds for the number 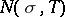 of zeros of
of zeros of 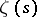 and for the number
and for the number 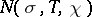 of zeros of
of zeros of  in the rectangle
in the rectangle 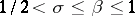 ,
, 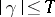 . The density method is substantially based on these theorems, which have been called density theorems.
. The density method is substantially based on these theorems, which have been called density theorems.
G. Hoheisel (1930) was the first to use the density method with density theorems for 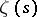 in order to estimate the difference between two adjacent prime numbers. He was able to show that there is a positive constant
in order to estimate the difference between two adjacent prime numbers. He was able to show that there is a positive constant 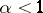 such that for
such that for 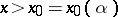 there is always a prime number between
there is always a prime number between  and
and 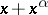 . Subsequently, any improvement in the bound for
. Subsequently, any improvement in the bound for  led to a more precise constant
led to a more precise constant 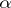 . Yu.V. Linnik (1944 and subsequent years) developed the density method for Dirichlet
. Yu.V. Linnik (1944 and subsequent years) developed the density method for Dirichlet 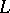 -functions; he was the first to examine the distributions of the zeros of
-functions; he was the first to examine the distributions of the zeros of 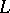 -functions for variable
-functions for variable 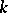 , and in particular obtained results on the "frequency" of the zeros of
, and in particular obtained results on the "frequency" of the zeros of  near the point
near the point 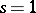 , which provided a bound for the least prime number
, which provided a bound for the least prime number 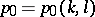 in the arithmetic progression
in the arithmetic progression 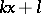 ,
,  ,
, 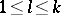 ,
, 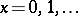 :
:  , where
, where  is some absolute constant. Improving the bounds on
is some absolute constant. Improving the bounds on 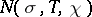 leads to a more precise constant
leads to a more precise constant  . Linnik, in applying density theorems for
. Linnik, in applying density theorems for 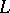 -functions, derived a new proof of Vinogradov's theorem on the representation of any sufficiently large odd number as the sum of three prime numbers (see Goldbach problem).
-functions, derived a new proof of Vinogradov's theorem on the representation of any sufficiently large odd number as the sum of three prime numbers (see Goldbach problem).
The density method in the theory of 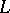 -functions has provided a strong result in the binary Goldbach problem: Any sufficiently large natural number can be represented as the sum of two prime numbers and some power of two bounded by an absolute constant.
-functions has provided a strong result in the binary Goldbach problem: Any sufficiently large natural number can be represented as the sum of two prime numbers and some power of two bounded by an absolute constant.
The strongest results from the density method are obtained in combination with other methods, in particular with the method of the large sieve. The Vinogradov–Bombieri theorem (1965), which in many cases replaces the generalized Riemann hypothesis (cf. Riemann hypothesis, generalized) was proved in this way. The ideas and results from the density method can be transferred from the field of rational numbers to an algebraic number field.
References
| [1] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [2] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [3] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
Comments
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
Density method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_method&oldid=18483