Denjoy integral
The narrow (special) Denjoy integral is a generalization of the Lebesgue integral. A function 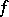 is said to be integrable in the sense of the narrow (special,
is said to be integrable in the sense of the narrow (special, 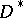 ) Denjoy integral on
) Denjoy integral on 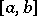 if there exists a continuous function
if there exists a continuous function 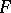 on
on 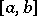 such that
such that 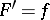 almost everywhere, and if for any perfect set
almost everywhere, and if for any perfect set 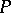 there exists a portion of
there exists a portion of 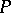 on which
on which 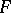 is absolutely continuous and where
is absolutely continuous and where
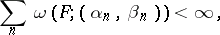 |
where 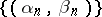 is the totality of intervals contiguous to that portion of
is the totality of intervals contiguous to that portion of 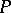 and
and 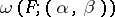 is the oscillation of
is the oscillation of 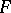 on
on 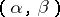 ;
;
 |
This generalization of the Lebesgue integral was introduced by A. Denjoy
who showed that his integral reproduces the function with respect to its pointwise finite derivative. The 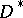 integral is equivalent to the Perron integral.
integral is equivalent to the Perron integral.
The wide (general) Denjoy integral is a generalization of the narrow Denjoy integral. A function 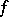 is said to be integrable in the sense of the wide (general,
is said to be integrable in the sense of the wide (general, 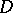 ) Denjoy integral on
) Denjoy integral on 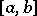 if there exists a continuous function
if there exists a continuous function 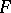 on
on 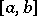 such that its approximate derivative is almost everywhere equal to
such that its approximate derivative is almost everywhere equal to 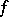 and if, for any perfect set
and if, for any perfect set 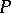 , there exists a portion of
, there exists a portion of 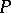 on which
on which 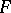 is absolutely continuous; here
is absolutely continuous; here
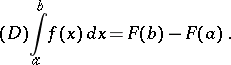 |
Introduced independently, and almost at the same time, by Denjoy
and A.Ya. Khinchin , . The  integral reproduces a continuous function with respect to its pointwise finite approximate derivative.
integral reproduces a continuous function with respect to its pointwise finite approximate derivative.
A totalization  is a constructively defined integral for solving the problem of constructing a generalized Lebesgue integral which would permit one to treat any convergent trigonometric series as a Fourier series (with respect to this integral). Introduced by Denjoy .
is a constructively defined integral for solving the problem of constructing a generalized Lebesgue integral which would permit one to treat any convergent trigonometric series as a Fourier series (with respect to this integral). Introduced by Denjoy .
A totalization 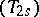 differs from a totalization
differs from a totalization 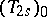 by the fact that the definition of the latter totalization involves an approximate rather than an ordinary limit. Denjoy [5] also gave a descriptive definition of a totalization
by the fact that the definition of the latter totalization involves an approximate rather than an ordinary limit. Denjoy [5] also gave a descriptive definition of a totalization 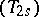 . For relations between
. For relations between 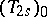 and
and 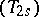 and other integrals, see [6].
and other integrals, see [6].
References
| [1a] | A. Denjoy, "Une extension de l'integrale de M. Lebesgue" C.R. Acad. Sci. , 154 (1912) pp. 859–862 |
| [1b] | A. Denjoy, "Calcul de la primitive de la fonction dérivée la plus générale" C.R. Acad. Sci. , 154 (1912) pp. 1075–1078 |
| [2] | A. Denjoy, "Sur la dérivation et son calcul inverse" C.R. Acad. Sci. , 162 (1916) pp. 377–380 |
| [3] | A.Ya. [A.Ya. Khinchin] Khintchine, "Sur une extension de l'integrale de M. Denjoy" C.R. Acad. Sci. , 162 (1916) pp. 287–291 |
| [4] | A.Ya. Khinchin, "On the process of Denjoy integration" Mat. Sb. , 30 (1918) pp. 543–557 (In Russian) |
| [5] | A. Denjoy, "Leçons sur le calcul des coefficients d'une série trigonométrique" , 1–4 , Gauthier-Villars (1941–1949) |
| [6] | I.A. Vinogradova, V.A. Skvortsov, "Generalized Fourier series and integrals" J. Soviet Math. , 1 (1973) pp. 677–703 Itogi Nauk. Mat. Anal. 1970 (1971) pp. 65–107 |
| [7] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
Comments
Just as the Lebesgue integral allows one to compute the mass corresponding to some density function, the Denjoy integral (called totalization by Denjoy also in the case 1) or 2)) allows one to compute the primitive (defined up to a constant) of some function. And, whereas for smooth functions calculating primitives is the usual way of calculating masses, in the general case the calculus of primitives (in the sense of 1) or 2)) depends on and is more involved than the calculus of masses. Denjoy gave a constructive scheme (one for 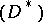 and a similar one for
and a similar one for 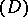 ) to calculate when possible the totalization
) to calculate when possible the totalization 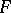 of a function
of a function 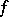 by induction over the countable ordinal numbers, something which does not exist for similar integrals like Perron's integral: If
by induction over the countable ordinal numbers, something which does not exist for similar integrals like Perron's integral: If 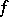 has a totalization (for example, if
has a totalization (for example, if  is the derivative in case 1), or the approximate derivative in case 2), of some function) the construction stops at some countable ordinal number and gives
is the derivative in case 1), or the approximate derivative in case 2), of some function) the construction stops at some countable ordinal number and gives 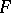 ; if
; if 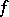 does not have a totalization, the construction never stops before
does not have a totalization, the construction never stops before 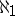 . This constructive scheme uses the Lebesgue integral, and two ways of defining "improper" integrals coming from the theory of the Riemann integral for unbounded functions and due, respectively, to A.L. Cauchy and A. Harnack. For details see [7] or [a1].
. This constructive scheme uses the Lebesgue integral, and two ways of defining "improper" integrals coming from the theory of the Riemann integral for unbounded functions and due, respectively, to A.L. Cauchy and A. Harnack. For details see [7] or [a1].
References
| [a1] | G. Choquet, "Outils topologiques et métriques de l'analyse mathématique" , Centre Docum. Univ. Paris (1969) (Rédigé par C. Mayer) |
Denjoy integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Denjoy_integral&oldid=12910