Dendritic manifold

A smooth odd-dimensional manifold of a special type which is the boundary of an even-dimensional manifold constructed from fibrations over spheres by a glueing scheme specified by some graph (tree).

Let 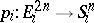, 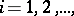be a fibration over -spheres with as fibre the -ball 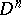and as structure group the group 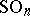, and let 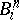be the closed standard -ball in the -sphere 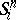; then

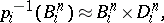where 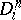is the fibre 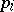. Let

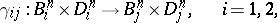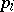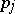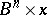be a homeomorphism realizing the glueing of two fibrations , and mapping each -ball from 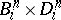into some ball 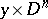from 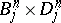(the glueing alters the factors of the direct product 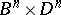). The result of glueing two fibrations 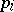, 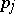is the 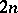-dimensional manifold 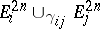which, as a result of "angle smoothing" , is converted to a smooth manifold.

The fibrations 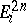are considered as "structural blocks" from which it is possible to construct, by pairwise glueing, the resulting smooth manifold as follows. Let 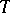be a one-dimensional finite complex (a graph). Each vertex of is brought into correspondence with a block 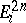; next, 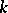, 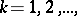non-intersecting -balls 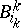are selected in 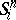, where 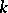is equal to the branching index of the respective vertex, and the glueing is performed according to the scheme indicated by 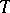. The manifold with boundary thus obtained is denoted by 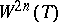(neglecting the dependence on the choice o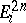f ). If 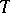is a tree, and therefore the graph is without cycles, the boundary 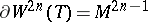is said to be a dendritic manifold.

If 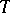is a tree, 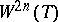has the homotopy type of a bouquet of 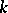spheres, where 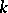is the number of vertices of .

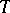The dendritic manifold 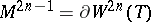is an integral homology 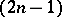-sphere if and only if the determinant of the matrix of the integral bilinear intersection 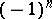-form defined on the lattice of -dimensional homology groups 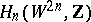equals 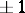. If this condition is met, the manifold 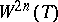is called a plumbing.

If 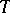is a tree and 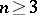, 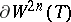is simply connected; if 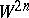is a plumbing, the boundary 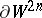is a homotopy sphere if .

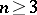If the plumbing 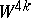is parallelizable, the diagonal of the intersection matrix of 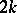-dimensional cycles is occupied by even numbers; in such a case the signature of the intersection matrix is divisible by 8. The plumbing 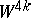is parallelizable if and only if all the fibrations over 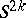used in constructing 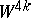are stably trivial; e.g., if all fibrations used in constructing 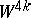are tangent bundles on discs over 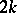-dimensional spheres, the plumbing 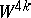is parallelizable. The plumbing 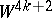will be parallelizable if and only if any fibration 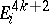used as a block in the construction of 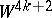is either trivial or is a tubular neighbourhood of the diagonal in the product 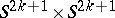, i.e. is a tangent bundle on discs over 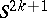. If the plumbing 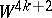is parallelizable, its intersection matrix can be reduced to the symplectic form consisting of blocks

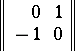situated along the main diagonal.

Especially important plumbings are the Milnor manifolds of dimension 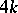, , 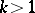and the Kervaire manifolds of dimension 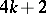, 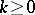. The Milnor manifolds are constructed as follows: A few copies of the tubular neighbourhood 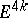of the diagonal in the product 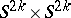are taken as blocks, while the graph 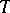is of the form

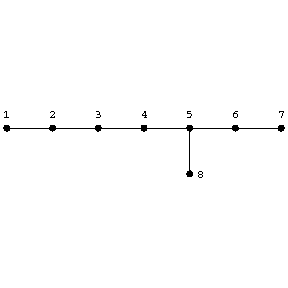
Figure: d031010a

Under these conditions the manifold 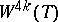realizes a quadratic form of order eight, in which every element on the main diagonal equals 2, while the signature equals 8.

In constructing the Kervaire manifolds 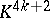one takes two copies of the block obtained as the tubular neighbourhood 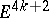of the diagonal in the product 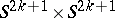. They are glued together so that the intersection matrix has the form

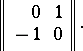The boundary of a Milnor manifold 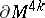(a Milnor sphere) is never diffeomorphic to the standard sphere 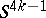. As regards Kervaire manifolds, this problem has not yet (1987) been conclusively solved. If 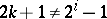, then the boundary of a Kervaire manifold 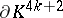(a Kervaire sphere) is always non-standard; if 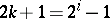, one obtains the standard sphere 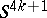for 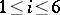, while for other 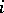it remains unsolved (cf. Kervaire invariant).

The Kervaire manifolds 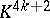of dimension 2, 6 or 14 are products of spheres 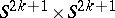, 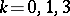respectively, after an open cell has been discarded, while all other Kervaire manifolds are not homeomorphic to the products of spheres with a discarded cell.

The PL-manifolds 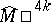and 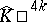are often used in the topology of manifolds. These manifolds are obtained by adding a cone over the boundary of, respectively, the Milnor manifolds and the Kervaire manifolds 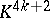. In the theory of four-dimensional manifolds a certain simply-connected almost-parallelizable manifold 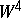(usually called a Rokhlin manifold) plays an especially important role; its signature is 16, cf. [6]. In the known examples of Rokhlin manifolds, the minimum value of the two-dimensional Betti number is 22. The second manifold is 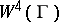, where 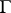is the graph indicated above, and the tubular neighbourhood of the diagonal in the product 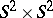is taken as the block. The boundary of the manifold 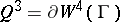thus obtained is a dodecahedral space which is not simply connected.

The three-dimensional dendritic manifolds 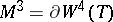belong to the class of so-called Seifert manifolds. Not all three-dimensional manifolds are dendritic manifolds; the Poincaré conjecture holds for dendritic manifolds. In particular, three-dimensional lens spaces (cf. Lens space) are obtained by glueing two blocks only.

References

[1]	M. Kervaire, "A manifold which does not admit any differentiable structure" Comment. Math. Helv. , 34 (1960) pp. 257–270
[2]	M. Kervaire, J. Milnor, "Groups of homotopy spheres. I" Ann. of Math. , 77 : 3 (1963) pp. 504–537
[3]	J.W. Milnor, "Differential topology" , Lectures on modern mathematics , II , Wiley (1964) pp. 165–183
[4]	F. Hirzebruch, W.D. Neumann, S.S. Koh, "Differentiable manifolds and quadratic forms" , M. Dekker (1971)
[5]	W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972)
[6]	R. Mandelbaum, "Four-dimensional topology: an introduction" Bull. Amer. Math. Soc. , 2 : 1 (1980) pp. 1–159

Comments

The technique described in the article above and leading to so-called "dendritic manifolds" (a phrase not often used in the West) is known as surgery, plumbing or as the technique of spherical modification.