Dempster-Shafer theory
mathematical theory of evidence, belief function theory
A theory initiated by A.P. Dempster [a2] and later developed by G. Shafer [a6]. It deals with the representation of non-probabilistic uncertainty about sets of facts (belief function) and the accumulation of "evidence" stemming from independent sources (Dempster's rule of evidence combination) and with reasoning under incomplete information (Dempster's rule of conditioning); see below. Extensions to infinite countable sets and continuous sets have been studied. However, below finite sets of facts (elementary events) are considered.
As with probability theory, four different approaches to handling Dempster–Shafer theory may be distinguished: the axiomatic approach (formal properties of belief functions are analyzed); the naive case-based approach (a direct case-based interpretation of properties of belief functions is sought); the in-the-limit approach (properties of the belief function are considered as in-the-limit properties of sets of cases); and the subjectivist approach (predominantly, the qualitative behaviour of subjectively assigned beliefs is studied, no case-based interpretation is sought and belief is considered as a subjective basis for decision-making).
Axiomatic approach.
Let  be a finite set of elements, called elementary events. Any subset of
be a finite set of elements, called elementary events. Any subset of  with cardinality
with cardinality  is also called a frame of discernment and any other subset of
is also called a frame of discernment and any other subset of  is called a composite event.
is called a composite event.
The central concept of a belief function is understood as any function  fulfilling the axioms:
fulfilling the axioms:
 ;
;
 ;
;

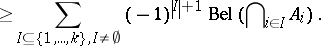 |
Due to the last axiom, a belief function 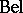 is actually a Choquet capacity, monotone of infinite order (cf. also Capacity). By introducing the so-called basic probability assignment function (bpa function), or mass function,
is actually a Choquet capacity, monotone of infinite order (cf. also Capacity). By introducing the so-called basic probability assignment function (bpa function), or mass function, 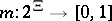 such that
such that 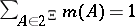 and
and 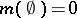 , then
, then 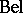 can be expressed as
can be expressed as 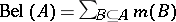 . Other uncertainty measures can also be defined, like the plausibility function
. Other uncertainty measures can also be defined, like the plausibility function  and the commonality function
and the commonality function 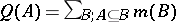 . Given one of these functions
. Given one of these functions  ,
,  ,
, 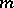 ,
,  , any other of them may be deterministically derived. Hence the function
, any other of them may be deterministically derived. Hence the function  is frequently used in the definition of further concepts, e.g., any set
is frequently used in the definition of further concepts, e.g., any set 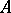 with
with 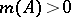 is called a focal point of the belief function. If
is called a focal point of the belief function. If 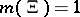 , then the belief function is called vacuous.
, then the belief function is called vacuous.
Another central concept, the rule of combination of two independent belief functions 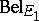 ,
,  over the same frame of discernment (the so-called Dempster rule of evidence combination), denoted by
over the same frame of discernment (the so-called Dempster rule of evidence combination), denoted by 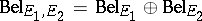 , is defined as follows:
, is defined as follows:
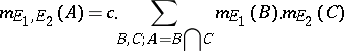 |
(with  a constant normalizing the sum of
a constant normalizing the sum of 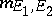 to
to 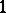 ).
).
Suppose that a frame of discernment 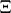 is equal to the cross product of domains
is equal to the cross product of domains 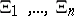 , with
, with  discrete variables
discrete variables 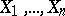 spanning the space
spanning the space 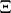 . Let
. Let 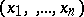 be a vector in the space spanned by the variables
be a vector in the space spanned by the variables  . Its projection onto the subspace spanned by the variables
. Its projection onto the subspace spanned by the variables  (with
(with 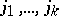 distinct indices from
distinct indices from 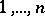 ) is then the vector
) is then the vector 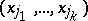 . The vector
. The vector  is also called an extension of
is also called an extension of  . The projection of a set
. The projection of a set 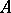 of such vectors is the set
of such vectors is the set 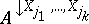 of projections of all individual vectors from
of projections of all individual vectors from 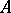 onto
onto  .
. 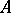 is also called an extension of
is also called an extension of 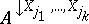 .
.  is called a vacuous extension of
is called a vacuous extension of 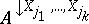 if (and only if)
if (and only if) 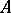 contains all possible extensions of each individual vector in
contains all possible extensions of each individual vector in 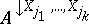 . The fact that
. The fact that  is a vacuous extension of
is a vacuous extension of  onto
onto 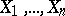 is denoted by
is denoted by 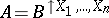 .
.
Let  be a basic probability assignment function on the space of discernment spanned by the set of variables
be a basic probability assignment function on the space of discernment spanned by the set of variables 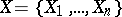 , and let
, and let 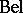 be the corresponding belief function. Let
be the corresponding belief function. Let  be a subset of
be a subset of 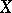 . The projection operator (or marginalization operator)
. The projection operator (or marginalization operator) 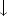 of
of  (or
(or  ) onto the subspace spanned by
) onto the subspace spanned by 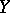 is defined as
is defined as
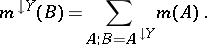 |
The vacuous extension operator 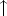 of
of  (or
(or 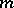 ) from
) from  onto the superspace spanned by
onto the superspace spanned by 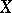 is defined as follows: for any
is defined as follows: for any 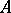 in
in  and any
and any 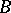 in
in 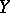 such that
such that  one has
one has 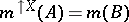 , and for any other
, and for any other 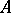 from
from 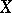 ,
,  . To denote that a belief function
. To denote that a belief function 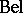 is defined over the space spanned by the set of variables
is defined over the space spanned by the set of variables  one frequently writes
one frequently writes  . By convention, if one wants to combine, using Dempster's rule, two belief functions not sharing the frame of discernment, then one looks for the closest common vacuous extension of their frames of discernment without explicitly mentioning this.
. By convention, if one wants to combine, using Dempster's rule, two belief functions not sharing the frame of discernment, then one looks for the closest common vacuous extension of their frames of discernment without explicitly mentioning this.
The last important concept of Dempster–Shafer theory is the Dempster rule of conditioning: Let 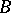 be a subset of
be a subset of  , called evidence, and let
, called evidence, and let 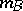 be a basic probability assignment such that
be a basic probability assignment such that 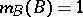 and
and 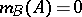 for all
for all  different from
different from 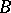 . Then the conditional belief function
. Then the conditional belief function  , representing the belief function
, representing the belief function 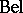 conditioned on evidence
conditioned on evidence 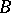 , is defined as:
, is defined as:
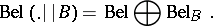 |
The conditioning as defined by the above rule is the foundation of reasoning in Dempster–Shafer theory: One starts with a belief function 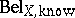 defined in a multi-variable space
defined in a multi-variable space  (being one's knowledge), makes certain observations on the values taken by some observational variables
(being one's knowledge), makes certain observations on the values taken by some observational variables 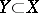 , e.g.
, e.g. 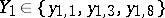 , denotes this knowledge by
, denotes this knowledge by 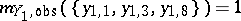 , and then one wishes to know what value will be taken by a predicted variable
, and then one wishes to know what value will be taken by a predicted variable  . To that end one calculates the belief for the predicted variable as
. To that end one calculates the belief for the predicted variable as
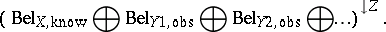 |
Due to the large space, the calculation of such a margin is prohibitive unless one can decompose 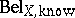 into a set of "smaller" belief functions
into a set of "smaller" belief functions 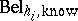 over a set
over a set 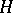 of subsets of
of subsets of  such that
such that
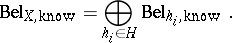 |
The set 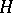 is hence a hypergraph. If
is hence a hypergraph. If  is a hypertree (a special type of hypergraph), then one can efficiently reason using the Shenoy–Shafer algorithms [a7]. Any hypergraph can be transformed into a hypertree, but the task aiming to obtain the best hypertree for reasoning (with smallest subsets in
is a hypertree (a special type of hypergraph), then one can efficiently reason using the Shenoy–Shafer algorithms [a7]. Any hypergraph can be transformed into a hypertree, but the task aiming to obtain the best hypertree for reasoning (with smallest subsets in 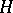 ) is prohibitive (
) is prohibitive (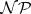 -hard, cf. also
-hard, cf. also 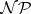 ), hence suboptimal solutions are elaborated. In the Shenoy–Shafer framework, both forward, backward and mixed reasoning is possible.
), hence suboptimal solutions are elaborated. In the Shenoy–Shafer framework, both forward, backward and mixed reasoning is possible.
Note that in the above decomposition it is not assumed that the 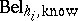 can be calculated in any way from
can be calculated in any way from 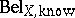 . As
. As 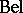 is known to have so-called graphoidal properties [a8], a decomposition similar to Bayesian networks for probability distributions has also been studied. An a priori-condition belief function
is known to have so-called graphoidal properties [a8], a decomposition similar to Bayesian networks for probability distributions has also been studied. An a priori-condition belief function 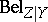 of variables
of variables 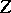 given
given 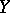 (defined over
(defined over 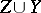 ), both sets with empty intersection and both subsets of
), both sets with empty intersection and both subsets of 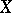 , is introduced as:
, is introduced as:
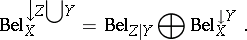 |
In general, many such functions may exist. In these settings one says that for a belief function 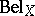 two non-intersecting sets of variables
two non-intersecting sets of variables 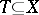 and
and 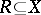 are independent given
are independent given 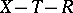 if
if
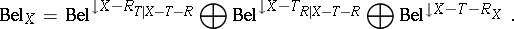 |
The a priori-conditional belief function is usually not a belief function, as it usually does not match the third axiom for belief functions, and even may take negative values (and so do the corresponding plausibility and mass functions). Only conditional commonality functions are always non-negative everywhere. As a partial remedy, the so-called 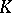 function has been proposed:
function has been proposed:
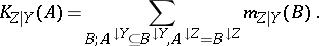 |
It may be viewed as an analogue of the true mass function for "a priori conditionals" , as it is non-negative and for any fixed value of  the sum over
the sum over 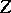 equals
equals  . Contrary to intuitions with probability distributions, the combination of an a priori conditional belief function with a (true) belief function by Dempster's rule need not lead to a belief function. Hence such a priori functions are poorly investigated so far (2000).
. Contrary to intuitions with probability distributions, the combination of an a priori conditional belief function with a (true) belief function by Dempster's rule need not lead to a belief function. Hence such a priori functions are poorly investigated so far (2000).
Naive case-based approach.
Currently (as of 2000), at least three naive case-based models compatible with the definition of belief function, Dempster's rule of evidence combination and Dempster 's rule of conditioning exist: the marginally correct approximation, the qualitative model and the quantitative model.
Marginally correct approximation.
This approach [a3] assumes that the belief function shall constitute lower bounds for frequencies; however, only for the marginals and not for the joint distribution. Then the reasoning process is expressed in terms of so-called Cano conditionals [a1] — a special class of a priori conditional belief functions that are everywhere non-negative. As for a general belief function, the Cano conditionals usually do not exist, they have to be calculated as an approximation to the actual a priori conditional belief function. This approach involves a modification of the reasoning mechanism, because the correctness is maintained only by reasoning forward. Depending on the reasoning direction, one needs different "Markov trees" for the reasoning engine.
Qualitative approach.
This approach [a4] is based on earlier rough set interpretations in Dempster–Shafer theory [a9], but makes a small and still significant distinction. All computations are carried out in a strictly "relational" way, i.e. indistinguishable objects in a database are merged (no object identities). The behaviour under reasoning fits strictly into the reasoning model of Dempster–Shafer theory. Factors of the hypergraph representation can be expressed by relational tables. Conditional independence is well defined. However, there is no interpretation for conditional belief functions in this model.
Quantitative approach.
The quantitative model [a5], [a11] assumes that during the reasoning process one attaches labels to objects, hiding some of their properties. There is a full agreement with the reasoning mechanism of Dempster–Shafer theory (in particular, Dempster's rule of conditioning). When combining two independent belief functions, only in the limit agreement with Dempster's rule of evidence combination can be achieved. Conditional independence and conditional belief functions are well defined. Processes have also been elaborated that, in the limit, can give rise to well-controlled graphoidally structured belief functions, and learning procedures for the discovery of graphoidal structures from data have been elaborated. The quantitative model seems to be the model best fitting for belief functions.
Subjectivist approach.
One assumes that among the elements of the set  , called "worlds" , one world corresponds to the "actual world" . There is an agent who does not know which world is the actual world and who can only express the strength of his/her opinion (called the degree of belief) that the actual world belongs to a certain subset of
, called "worlds" , one world corresponds to the "actual world" . There is an agent who does not know which world is the actual world and who can only express the strength of his/her opinion (called the degree of belief) that the actual world belongs to a certain subset of  . One such approach is the so-called transferable belief model [a10]. Besides the two already mentioned rules of Dempster (combination and conditioning), many more rules handling various sources of evidence have been added, including disjunctive rules of combination, alpha-junctions rules, cautious rules, pignistic transformation, a specialization concept, a measure of information content, canonical decomposition, concepts of confidence and diffidence, and a generalized Bayesian theorem. Predominantly, the qualitative behaviour of subjectively assigned beliefs is studied. So far (as of 2000), no attempt paralleling the subjective probability approach of B. de Finetti has been made to bridge the gap between subjective belief assignment and observed frequencies.
. One such approach is the so-called transferable belief model [a10]. Besides the two already mentioned rules of Dempster (combination and conditioning), many more rules handling various sources of evidence have been added, including disjunctive rules of combination, alpha-junctions rules, cautious rules, pignistic transformation, a specialization concept, a measure of information content, canonical decomposition, concepts of confidence and diffidence, and a generalized Bayesian theorem. Predominantly, the qualitative behaviour of subjectively assigned beliefs is studied. So far (as of 2000), no attempt paralleling the subjective probability approach of B. de Finetti has been made to bridge the gap between subjective belief assignment and observed frequencies.
References
| [a1] | J. Cano, M. Delgado, S. Moral, "An axiomatic framework for propagating uncertainty in directed acyclic networks" Internat. J. Approximate Reasoning , 8 (1993) pp. 253–280 |
| [a2] | A.P. Dempster, "Upper and lower probabilities induced by a multi-valued mapping" Ann. Math. Stat. , 38 (1967) pp. 325–339 |
| [a3] | M.A. Kłopotek, S.T. Wierzchoń, "On marginally correct approximations of Dempster–Shafer belief functions from data" , Proc. IPMU'96 (Information Processing and Management of Uncertainty), Grenada (Spain), 1-5 July , II , Univ. Granada (1996) pp. 769–774 |
| [a4] | M.A. Kłopotek, S.T. Wierzchoń, "Qualitative versus quantitative interpretation of the mathematical theory of evidence" Z.W.Raś (ed.) A. Skowron (ed.) , Foundations of Intelligent Systems 7. Proc. ISMIS'97 (Charlotte NC, 15-17 Oct., 1997) , Lecture Notes in Artificial Intelligence , 1325 , Springer (1997) pp. 391–400 |
| [a5] | M.A. Kłopotek, "On (anti)conditional independence in Dempster–Shafer theory" J. Mathware and Softcomputing , 5 : 1 (1998) pp. 69–89 |
| [a6] | G. Shafer, "A mathematical theory of evidence" , Princeton Univ. Press (1976) |
| [a7] | P. Shenoy, G. Shafer, "Axioms for probability and belief-function propagation" R.D. Shachter (ed.) T.S. Levitt (ed.) L.N. Kanal (ed.) J.F. Lemmer (ed.) , Uncertainty in Artificial Intelligence , 4 , Elsevier (1990) |
| [a8] | P.P. Shenoy, "Conditional independence in valuation based systems" Internat. J. Approximate Reasoning , 109 (1994) |
| [a9] | A. Skowron, J.W. Grzymała-Busse, "From rough set theory to evidence theory" R.R. Yager (ed.) J. Kasprzyk (ed.) M. Fedrizzi (ed.) , Advances in the Dempster–Shafer Theory of Evidence , Wiley (1994) pp. 193–236 |
| [a10] | Ph. Smets, "Numerical representation of uncertainty" D.M. Gabbay (ed.) Ph. Smets (ed.) , Handbook of Defeasible Reasoning and Uncertainty Management Systems , 3 , Kluwer Acad. Publ. (1998) pp. 265–309 |
| [a11] | S.T. Wierzchoń, M.A. Kłopotek, "Modified component valuations in valuation based systems as a way to optimize query processing" J. Intelligent Information Syst. , 9 (1997) pp. 157–180 |
Dempster-Shafer theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dempster-Shafer_theory&oldid=17440