Deligne-Lusztig characters
Characters occurring in the context of the representation theory of finite reductive groups (cf. also Finite group, representation of a). Such groups arise as subgroups of connected reductive algebraic groups 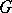 (cf. also Reductive group) invariant under a Frobenius morphism
(cf. also Reductive group) invariant under a Frobenius morphism 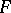 . The fixed-point subgroups
. The fixed-point subgroups 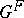 are the finite groups of Lie type.
are the finite groups of Lie type.
P. Deligne and G. Lusztig made a fundamental advance in determining the irreducible characters of the groups 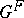 over an algebraically closed field of characteristic
over an algebraically closed field of characteristic  . They constructed generalized characters
. They constructed generalized characters 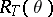 of
of  (i.e.
(i.e. 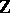 -combinations of irreducible characters) parametrized by an
-combinations of irreducible characters) parametrized by an 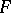 -stable maximal torus
-stable maximal torus 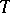 of
of 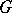 and an irreducible character
and an irreducible character 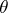 of
of 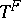 . If
. If  is in general position,
is in general position, 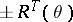 is an irreducible character of
is an irreducible character of 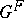 . The existence of such families of irreducible characters parametrized by characters of maximal tori had previously been conjectured by I. Macdonald. In order to obtain the remaining irreducible characters of
. The existence of such families of irreducible characters parametrized by characters of maximal tori had previously been conjectured by I. Macdonald. In order to obtain the remaining irreducible characters of 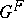 it is sufficient to decompose all the
it is sufficient to decompose all the 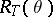 into
into 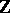 -combinations of irreducible characters, since each irreducible character appears as a component of some
-combinations of irreducible characters, since each irreducible character appears as a component of some  .
.
The Deligne–Lusztig generalized characters are defined in terms of the 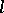 -adic cohomology with coefficients in a local system
-adic cohomology with coefficients in a local system  on an algebraic variety
on an algebraic variety 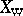 , called the Deligne–Lusztig variety. This depends on an element
, called the Deligne–Lusztig variety. This depends on an element 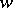 of the Weyl group
of the Weyl group 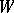 of
of  , such that the maximal torus
, such that the maximal torus 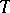 is obtained from a maximally split torus by twisting by the element
is obtained from a maximally split torus by twisting by the element 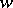 .
. 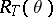 is the alternating sum of the traces on the
is the alternating sum of the traces on the 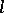 -adic cohomology groups
-adic cohomology groups 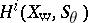 . Here,
. Here, 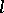 can be any prime number distinct from the characteristic of
can be any prime number distinct from the characteristic of 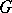 .
.
Deligne and Lusztig's original paper, in which the 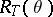 were defined, is [a4].
were defined, is [a4].
The way in which the 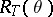 decompose into irreducible characters was subsequently determined by Lusztig. First consider the case when
decompose into irreducible characters was subsequently determined by Lusztig. First consider the case when 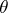 is the unit character. Components of characters
is the unit character. Components of characters 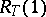 are called unipotent characters. It was shown by Lusztig that the unipotent characters fall into families, each family being associated with a certain irreducible representation of the Weyl group
are called unipotent characters. It was shown by Lusztig that the unipotent characters fall into families, each family being associated with a certain irreducible representation of the Weyl group 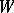 , called a special representation. The special representations are in bijective correspondence with the two-sided cells of
, called a special representation. The special representations are in bijective correspondence with the two-sided cells of 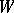 . The way in which the generalized characters
. The way in which the generalized characters 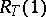 decompose into irreducible unipotent characters is related to the representation theory of the Weyl group, and can be determined explicitly.
decompose into irreducible unipotent characters is related to the representation theory of the Weyl group, and can be determined explicitly.
Consider now the case of an arbitrary irreducible character 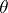 of
of 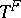 . There is a family of irreducible characters of
. There is a family of irreducible characters of  , called the semi-simple characters, which can be obtained as simple linear combinations of the
, called the semi-simple characters, which can be obtained as simple linear combinations of the 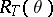 . The semi-simple characters have degree prime to the characteristic of
. The semi-simple characters have degree prime to the characteristic of 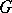 and are in natural bijective correspondence with the
and are in natural bijective correspondence with the  -stable conjugacy classes of semi-simple elements in the Langlands dual group
-stable conjugacy classes of semi-simple elements in the Langlands dual group 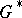 of
of 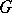 .
.
Consider now arbitrary irreducible characters of 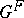 , not necessarily semi-simple or unipotent. Given any irreducible character of
, not necessarily semi-simple or unipotent. Given any irreducible character of 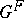 (cf. also Character of a group), there is an associated semi-simple character of
(cf. also Character of a group), there is an associated semi-simple character of  , which corresponds to a semi-simple class in
, which corresponds to a semi-simple class in 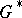 containing an
containing an 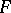 -stable element
-stable element  , and also a unipotent character of the centralizer of
, and also a unipotent character of the centralizer of  . This may be regarded as a Jordan decomposition of characters. The degree of the original irreducible character is the product of the degrees of the semi-simple and unipotent characters which it determines under the Jordan decomposition.
. This may be regarded as a Jordan decomposition of characters. The degree of the original irreducible character is the product of the degrees of the semi-simple and unipotent characters which it determines under the Jordan decomposition.
The description of the irreducible characters of the finite reductive groups can be found in [a6]. There are also accounts in [a2] and [a5].
The deeper results obtained by Lusztig on characters of 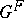 make use of
make use of 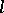 -adic intersection cohomology of the Deligne–Lusztig variety
-adic intersection cohomology of the Deligne–Lusztig variety  rather than ordinary
rather than ordinary 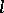 -adic cohomology. The generalized characters obtained from
-adic cohomology. The generalized characters obtained from 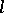 -adic intersection cohomology are related to those obtained from ordinary
-adic intersection cohomology are related to those obtained from ordinary 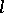 -adic cohomology by means of the Kazhdan–Lusztig polynomials, which had been introduced to obtain representations of Weyl groups and Iwahori–Hecke algebras. The advantage of working with
-adic cohomology by means of the Kazhdan–Lusztig polynomials, which had been introduced to obtain representations of Weyl groups and Iwahori–Hecke algebras. The advantage of working with 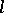 -adic intersection cohomology is that one can make use of the Deligne–Gabber purity theorem that the Frobenius
-adic intersection cohomology is that one can make use of the Deligne–Gabber purity theorem that the Frobenius 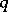 th power morphism acting on the
th power morphism acting on the 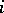 th intersection cohomology group has eigenvalues which all have absolute value
th intersection cohomology group has eigenvalues which all have absolute value 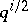 . An account of the way in which intersection cohomology can be used in representation theory can be found in [a9].
. An account of the way in which intersection cohomology can be used in representation theory can be found in [a9].
The algebraic groups 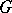 considered so far have been defined over an algebraically closed field of prime characteristic, so that one has a Frobenius morphism. However, Lusztig has used ideas on intersection cohomology to develop a "geometric theory of characters" which works equally well for reductive groups over arbitrary algebraically closed fields. This geometric theory of characters uses the theory of perverse sheaves, developed by A.A. Beilinson, J.N. Bernstein and P. Deligne in [a1]. The irreducible perverse sheaves are the intersection cohomology complexes. A character sheaf is a particular type of irreducible perverse sheaf. In the case of a reductive group over the algebraic closure of a finite field, a character sheaf fixed by the Frobenius mapping has a characteristic function which is a class function on the finite group
considered so far have been defined over an algebraically closed field of prime characteristic, so that one has a Frobenius morphism. However, Lusztig has used ideas on intersection cohomology to develop a "geometric theory of characters" which works equally well for reductive groups over arbitrary algebraically closed fields. This geometric theory of characters uses the theory of perverse sheaves, developed by A.A. Beilinson, J.N. Bernstein and P. Deligne in [a1]. The irreducible perverse sheaves are the intersection cohomology complexes. A character sheaf is a particular type of irreducible perverse sheaf. In the case of a reductive group over the algebraic closure of a finite field, a character sheaf fixed by the Frobenius mapping has a characteristic function which is a class function on the finite group 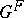 . These characteristic functions form an orthonormal basis of the set of class functions on
. These characteristic functions form an orthonormal basis of the set of class functions on 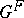 . They are not, in general, the irreducible characters of
. They are not, in general, the irreducible characters of 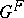 but are, roughly speaking, Fourier transforms of the irreducible characters. Thus, there is a close connection between the irreducible characters and the
but are, roughly speaking, Fourier transforms of the irreducible characters. Thus, there is a close connection between the irreducible characters and the  -stable irreducible character sheaves. However, since the theory of character sheaves is valid in the wider context of reductive groups over arbitrary algebraically closed fields, the ideas of the Deligne–Lusztig theory have an analogue in arbitrary connected reductive groups. An exposition of the theory of character sheaves can be found in [a10], [a11], [a12], [a13], while [a7], [a8] provide useful introductory material.
-stable irreducible character sheaves. However, since the theory of character sheaves is valid in the wider context of reductive groups over arbitrary algebraically closed fields, the ideas of the Deligne–Lusztig theory have an analogue in arbitrary connected reductive groups. An exposition of the theory of character sheaves can be found in [a10], [a11], [a12], [a13], while [a7], [a8] provide useful introductory material.
References
| [a1] | A.A. Beilinson, J.N. Bernstein, P. Deligne, "Faisceaux pervers" Astérisque , 100 (1982) |
| [a2] | R.W. Carter, "Finite groups of Lie type: Conjugacy classes and complex characters" , Wiley (1993) |
| [a3] | R.W. Carter, "On the representation theory of the finite groups of Lie type over an algebraically closed field of characteristic  " , Encylop. Math. Sci. , 77 , Springer (1996) " , Encylop. Math. Sci. , 77 , Springer (1996) |
| [a4] | P. Deligne, G. Lusztig, "Representations of reductive groups over finite fields" Ann. of Math. , 103 (1976) pp. 103–161 |
| [a5] | F. Digne, J. Michel, "Representations of finite groups of Lie type" , London Math. Soc. Student Texts , 21 , Cambridge Univ. Press (1991) |
| [a6] | G. Lusztig, "Characters of reductive groups over finite fields" , Ann. Math. Studies , 107 , Princeton Univ. Press (1984) |
| [a7] | G. Lusztig, "Intersection cohomology complexes on a reductive group" Invent. Math. , 75 (1984) pp. 205–272 |
| [a8] | G. Lusztig, "Introduction to character sheaves" , Proc. Symp. Pure Math. , 47 , Amer. Math. Soc. (1987) pp. 165–179 |
| [a9] | G. Lusztig, "Intersection cohomology methods in representation theory" I. Satake (ed.) , Proc. Internat. Congr. Math. Kyoto 1990 , I , Springer (1991) pp. 155–174 |
| [a10] | G. Lustzig, "Character sheaves I" Adv. Math. , 56 (1985) pp. 193–237 |
| [a11] | G. Lustzig, "Character sheaves II-III" Adv. Math. , 57 (1985) pp. 226–265; 266–315 |
| [a12] | G. Lustzig, "Character sheaves IV" Adv. Math. , 59 (1986) pp. 1–63 |
| [a13] | G. Lustzig, "Character sheaves V" Adv. Math. , 61 (1986) pp. 103–155 |
Deligne-Lusztig characters. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Deligne-Lusztig_characters&oldid=18390