Degenerate parabolic equation
From Encyclopedia of Mathematics
A partial differential equation
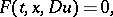 |
where the function  has the following property: For some even natural number
has the following property: For some even natural number  , all roots
, all roots  of the polynomial
of the polynomial
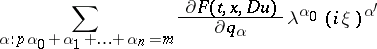 |
have non-positive real parts for all real  and, for certain
and, for certain  ,
,  ,
,  , and
, and  ,
, 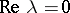 for some root
for some root 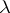 , or for certain
, or for certain 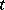 ,
,  and
and 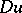 the leading coefficient at
the leading coefficient at  vanishes. Here
vanishes. Here 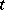 is an independent variable which is often interpreted as time;
is an independent variable which is often interpreted as time;  is an
is an  -dimensional vector
-dimensional vector 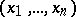 ;
;  is the unknown function;
is the unknown function; 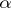 is a multi-index
is a multi-index 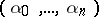 ;
;  is the vector with components
is the vector with components
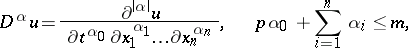 |
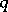 is a vector with components
is a vector with components  ,
, 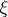 is an
is an  -dimensional vector
-dimensional vector 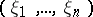 , and
, and 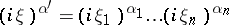 . See also Degenerate partial differential equation, and the references given there.
. See also Degenerate partial differential equation, and the references given there.
How to Cite This Entry:
Degenerate parabolic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_parabolic_equation&oldid=18826
Degenerate parabolic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_parabolic_equation&oldid=18826
This article was adapted from an original article by A.M. Il'in (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article