Degenerate hyperbolic equation
From Encyclopedia of Mathematics
A partial differential equation
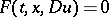 | (*) |
where the function  satisfies the following condition: The roots of the polynomial
satisfies the following condition: The roots of the polynomial
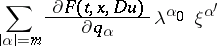 |
are real for all real  , and there exist
, and there exist  ,
,  ,
,  , and
, and  for which some of the roots either coincide or the coefficient of
for which some of the roots either coincide or the coefficient of  vanishes. Here
vanishes. Here 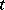 is an independent variable which is often interpreted as time;
is an independent variable which is often interpreted as time;  is an
is an  -dimensional vector
-dimensional vector 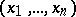 ;
;  is the unknown function;
is the unknown function; 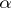 and
and 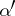 are multi-indices,
are multi-indices,  ,
,  ;
; 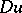 is a vector with components
is a vector with components
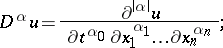 |
only derivatives of an order not exceeding  enter in equation (*); the
enter in equation (*); the 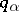 are the components of a vector
are the components of a vector 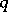 ;
;  is an
is an  -dimensional vector
-dimensional vector  ; and
; and  .
.
See also Degenerate partial differential equation and the references given there.
How to Cite This Entry:
Degenerate hyperbolic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_hyperbolic_equation&oldid=17807
Degenerate hyperbolic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_hyperbolic_equation&oldid=17807
This article was adapted from an original article by A.M. Il'in (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article