Deficiency subspace
defect subspace, defective subspace, of an operator
The orthogonal complement 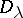 of the range of values
of the range of values 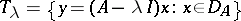 of the operator
of the operator 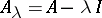 , where
, where 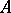 is a linear operator defined on a linear manifold
is a linear operator defined on a linear manifold  of a Hilbert space
of a Hilbert space  , while
, while  is a regular value (regular point) of
is a regular value (regular point) of 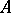 . Here, a regular value of an operator
. Here, a regular value of an operator 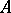 is understood to be a value of the parameter
is understood to be a value of the parameter 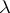 for which the equation
for which the equation  has a unique solution for any
has a unique solution for any 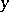 while the operator
while the operator 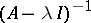 is bounded, i.e. the resolvent of
is bounded, i.e. the resolvent of 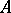 is bounded. As
is bounded. As  changes, the deficiency subspace
changes, the deficiency subspace 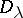 changes as well, but its dimension remains the same for all
changes as well, but its dimension remains the same for all 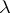 belonging to a connected component of the open set of all regular values of
belonging to a connected component of the open set of all regular values of 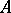 .
.
If 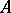 is a symmetric operator with a dense domain of definition
is a symmetric operator with a dense domain of definition  , its connected components of regular values will be the upper and the lower half-plane. In this case
, its connected components of regular values will be the upper and the lower half-plane. In this case 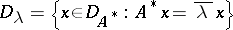 , while the deficiency numbers
, while the deficiency numbers 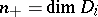 and
and 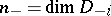 , where
, where 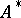 is the adjoint operator, are called the (positive and negative) deficiency indices of the operator
is the adjoint operator, are called the (positive and negative) deficiency indices of the operator  . In addition,
. In addition,
 |
i.e. 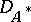 is the direct sum of
is the direct sum of 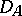 ,
, 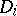 and
and 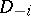 . Thus, if
. Thus, if 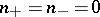 , the operator
, the operator 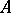 is self-adjoint; otherwise the deficiency subspace of a symmetric operator characterizes the extent of its deviation from a self-adjoint operator.
is self-adjoint; otherwise the deficiency subspace of a symmetric operator characterizes the extent of its deviation from a self-adjoint operator.
Deficiency subspaces play an important role in constructing the extensions of a symmetric operator to a maximal operator or to a self-adjoint (hyper-maximal) operator.
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) |
| [2] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in a Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators" , 1–2 , Interscience (1958–1963) |
| [4] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
Comments
The definition of a regular value of an operator as given above is not quite correct and should read as follows. The value 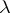 is a regular value of
is a regular value of  if there exists a positive number
if there exists a positive number 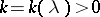 such that
such that 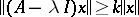 for all
for all 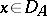 . In that case the kernel of
. In that case the kernel of 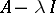 consists of the zero vector only and the image of
consists of the zero vector only and the image of 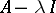 is closed (but not necessarily equal to the whole space).
is closed (but not necessarily equal to the whole space).
Deficiency subspace. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Deficiency_subspace&oldid=15718