Defect group of a block
Let 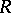 be a commutative ring, let
be a commutative ring, let 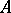 be an
be an 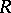 -algebra, and let
-algebra, and let 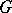 be a group. Then
be a group. Then 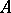 is said to be
is said to be 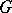 -algebra if
-algebra if 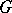 acts as a group of
acts as a group of 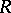 -algebra automorphisms of
-algebra automorphisms of 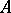 . Expressed otherwise, each
. Expressed otherwise, each 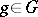 acts on each
acts on each 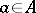 to give
to give  such that this
such that this 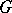 -action makes
-action makes 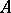 into a left
into a left 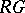 -module and
-module and 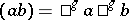 for all
for all 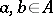 ,
, 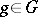 . Assume that
. Assume that 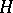 is a subgroup of
is a subgroup of 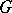 . It is customary to write
. It is customary to write 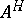 for the subalgebra of
for the subalgebra of 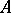 consisting of all
consisting of all 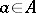 for which
for which  for all
for all 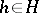 . The group algebra
. The group algebra 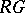 is a
is a 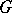 -algebra. Indeed, for any
-algebra. Indeed, for any 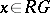 and
and 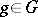 , define
, define  . Then
. Then 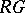 becomes a
becomes a 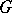 -algebra over
-algebra over 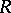 . Further examples of
. Further examples of 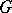 -algebras can be found in [a5].
-algebras can be found in [a5].
Let 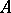 be a
be a 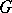 -algebra over
-algebra over 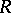 , where
, where 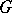 is a finite group, let
is a finite group, let 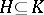 be subgroups of
be subgroups of 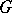 , and let
, and let 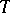 be a left transversal for
be a left transversal for  in
in 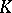 (i.e.,
(i.e., 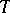 picks out one element in each (e.g., left) coset of
picks out one element in each (e.g., left) coset of 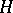 in
in 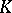 ; thus, it is a transversal of the system of subsets consisting of the (left) cosets; cf. also Combinatorial analysis). Then the mapping
; thus, it is a transversal of the system of subsets consisting of the (left) cosets; cf. also Combinatorial analysis). Then the mapping 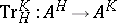 ,
, 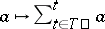 , is
, is 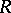 -linear and is independent of the choice of
-linear and is independent of the choice of 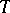 . It is customary to refer to
. It is customary to refer to 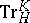 as the relative trace mapping and to denote the image of
as the relative trace mapping and to denote the image of 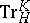 by
by 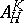 . Let
. Let  be a primitive idempotent of
be a primitive idempotent of 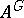 . A subgroup
. A subgroup 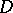 of
of 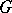 is called a defect group of
is called a defect group of  if
if 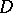 is a minimal element in the set of subgroups
is a minimal element in the set of subgroups 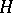 of
of 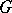 such that
such that 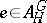 . Such a subgroup
. Such a subgroup 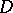 exists because the set of all subgroups
exists because the set of all subgroups  of
of 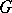 with
with 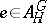 contains
contains 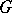 , and hence is non-empty. In the special case where
, and hence is non-empty. In the special case where 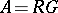 it is clear that
it is clear that  is a block idempotent of
is a block idempotent of 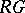 (cf. Block). For this reason the defect groups of
(cf. Block). For this reason the defect groups of  are also called the defect groups of the block
are also called the defect groups of the block 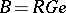 .
.
Again let 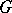 be a finite group, let
be a finite group, let 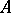 be a
be a 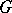 -algebra over
-algebra over 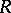 , and let
, and let  be a primitive idempotent of
be a primitive idempotent of 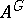 . Denote by
. Denote by 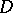 a defect group of
a defect group of  and assume that
and assume that 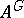 is semi-perfect (e.g.,
is semi-perfect (e.g., 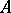 is a finitely generated
is a finitely generated 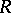 -module and
-module and 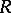 is a complete Noetherian semi-local ring, cf. also Noetherian ring; Local ring). If
is a complete Noetherian semi-local ring, cf. also Noetherian ring; Local ring). If 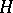 is a subgroup of
is a subgroup of 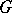 such that
such that 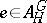 , then
, then 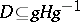 for some
for some 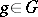 . Moreover, a subgroup
. Moreover, a subgroup 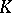 of
of 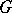 is a defect group of
is a defect group of  if and only if
if and only if 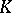 is
is 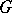 -conjugate to
-conjugate to 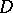 . In the most important case where
. In the most important case where 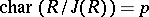 (
(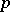 a prime number),
a prime number), 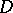 turns out to be a
turns out to be a 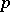 -subgroup of
-subgroup of 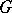 (see [a5]).
(see [a5]).
Let 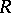 be a complete Noetherian semi-local ring such that
be a complete Noetherian semi-local ring such that 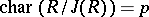 (
(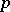 a prime number) and let
a prime number) and let 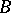 be a block of
be a block of 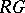 . Then a defect group of
. Then a defect group of 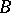 is a
is a 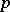 -subgroup of
-subgroup of 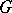 . Thus, if
. Thus, if 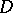 is a defect group of
is a defect group of 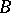 , then
, then 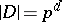 for some integer
for some integer 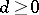 . The integer
. The integer 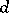 is called the defect of
is called the defect of 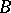 . The study of defect groups of blocks of
. The study of defect groups of blocks of 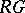 is especially important in the following cases:
is especially important in the following cases:
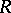 is a complete discrete valuation ring of characteristic
is a complete discrete valuation ring of characteristic  with
with 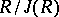 of prime characteristic
of prime characteristic 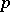 ;
;
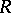 is a field of prime characteristic
is a field of prime characteristic 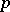 (see [a1], [a2], [a3], [a4], [a5]).
(see [a1], [a2], [a3], [a4], [a5]).
The ring-theoretic structure of blocks of 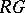 is closely related to the structure of their defect groups. The most extensive coverage of this topic can be found in [a5]. For various applications to the modular representation theory of groups, see also [a5]. There is no doubt that the current theory of defect groups of blocks will be significantly strengthened in the future, and that the field contains untapped reserves rich enough to ensure major strikes. For various open problems and the current (1996) state of the subject, see [a5].
is closely related to the structure of their defect groups. The most extensive coverage of this topic can be found in [a5]. For various applications to the modular representation theory of groups, see also [a5]. There is no doubt that the current theory of defect groups of blocks will be significantly strengthened in the future, and that the field contains untapped reserves rich enough to ensure major strikes. For various open problems and the current (1996) state of the subject, see [a5].
References
| [a1] | G. Karpilovsky, "Group representations" , 1 , North-Holland (1992) |
| [a2] | G. Karpilovsky, "Group representations" , 2 , North-Holland (1993) |
| [a3] | G. Karpilovsky, "Group representations" , 3 , North-Holland (1994) |
| [a4] | G. Karpilovsky, "Group representations" , 4 , North-Holland (1995) |
| [a5] | G. Karpilovsky, "Group representations" , 5 , North-Holland (1996) |
Defect group of a block. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Defect_group_of_a_block&oldid=14276