Dedekind theorem
From Encyclopedia of Mathematics
on the continuity of the real axis
For any cut 
of the set of real numbers (see Dedekind cut) there exists a real number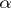 
which is either the largest in the class 
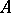or the smallest in the class 
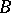. This statement is also known as the Dedekind principle (axiom) of continuity of the real axis (cf. Real number). The number 
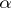is the least upper bound of 
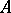and the greatest lower bound of 
.
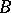How to Cite This Entry:
Dedekind theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_theorem&oldid=17055
Dedekind theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_theorem&oldid=17055
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article