Dedekind criterion (convergence of series)
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The series  , where
, where  and
and  are complex numbers, converges if the series
are complex numbers, converges if the series  converges absolutely,
converges absolutely,  , and if the partial sums of the series
, and if the partial sums of the series  are bounded.
are bounded.
Comments
The proof is based on the formula of summation by parts: Put  for
for  and
and  . Then for
. Then for  one has
one has
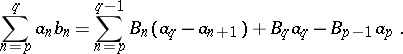 |
A related convergence criterion is the Dirichlet criterion (convergence of series).
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
How to Cite This Entry:
Dedekind criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_criterion_(convergence_of_series)&oldid=18271
Dedekind criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_criterion_(convergence_of_series)&oldid=18271
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article