Dedekind criterion (convergence of series)
From Encyclopedia of Mathematics
The series  , where
, where  and
and  are complex numbers, converges if the series
are complex numbers, converges if the series  converges absolutely,
converges absolutely,  , and if the partial sums of the series
, and if the partial sums of the series  are bounded.
are bounded.
Comments
The proof is based on the formula of summation by parts: Put  for
for  and
and  . Then for
. Then for  one has
one has
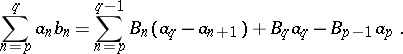 |
A related convergence criterion is the Dirichlet criterion (convergence of series).
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
How to Cite This Entry:
Dedekind criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_criterion_(convergence_of_series)&oldid=18271
Dedekind criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_criterion_(convergence_of_series)&oldid=18271
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article