De la Vallée-Poussin summation method
A method for summing series of numbers. It is denoted by the symbol 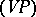 . A series
. A series
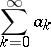 |
has a de la Vallée-Poussin sum 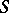 if the relation
if the relation
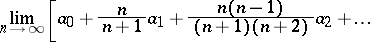 |
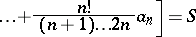 |
is valid. The method was proposed by Ch.J. de la Vallée-Poussin [1]. For the Fourier series of a function 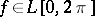 the de la Vallée-Poussin averages (see also de la Vallée-Poussin singular integral) are of the form
the de la Vallée-Poussin averages (see also de la Vallée-Poussin singular integral) are of the form
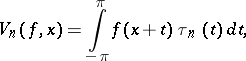 |
where
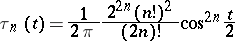 |
is the so-called de la Vallée-Poussin kernel. The de la Vallée-Poussin summation method is a regular summation method (cf. Regular summation methods). The method is stronger than all Cesàro summation methods (cf. Inclusion of summation methods). In view of its weak approximative properties, the de la Vallée-Poussin summation method is practically never used in the theory of approximation of functions.
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur l'approximation des fonctions d'une variable reélle et de leurs dérivées par des polynômes et des suites limitées de Fourier" Bull. Acad. Belg. , 3 (1908) pp. 193–254 |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [3] | T. Gronwall, "Ueber einige Summationsmethoden und ihre Anwendung auf die Fouriersche Reihe" J. Reine Angew. Math. , 147 (1917) pp. 16–35 |
De la Vallée-Poussin summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_summation_method&oldid=17703