The expression
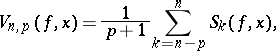 | (*) |
where 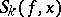 ,
, 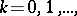 are the partial sums of the Fourier series of a function
are the partial sums of the Fourier series of a function 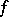 with period
with period 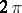 . If
. If 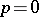 , the de la Vallée-Poussin sums become identical with the partial Fourier sums, and if
, the de la Vallée-Poussin sums become identical with the partial Fourier sums, and if  , they become identical with the Fejér sums (cf. Fejér sum). Ch.J. de la Vallée-Poussin [1], [2] was the first to study the method of approximating periodic functions by polynomials of the form (*); he also established the inequality
, they become identical with the Fejér sums (cf. Fejér sum). Ch.J. de la Vallée-Poussin [1], [2] was the first to study the method of approximating periodic functions by polynomials of the form (*); he also established the inequality
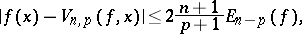 |
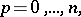 |
where 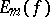 is the best uniform approximation of the function
is the best uniform approximation of the function 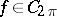 using trigonometric polynomials of order not greater than
using trigonometric polynomials of order not greater than 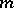 . If
. If 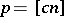 ,
, 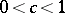 and
and 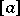 is the integer part of the number
is the integer part of the number  , the polynomials
, the polynomials 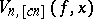 realize an approximation of order
realize an approximation of order 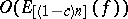 . The polynomials
. The polynomials 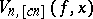 yield the best order approximations of continuous functions of period
yield the best order approximations of continuous functions of period 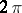 , with an estimate
, with an estimate 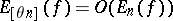 for certain values of
for certain values of 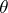 ,
, 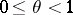 . The de la Vallée-Poussin sums have several properties which are of interest in the theory of summation of Fourier series. For instance, if
. The de la Vallée-Poussin sums have several properties which are of interest in the theory of summation of Fourier series. For instance, if 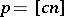 ,
, 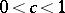 , then
, then 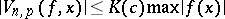 , and if
, and if 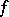 is a trigonometric polynomial of order not exceeding
is a trigonometric polynomial of order not exceeding 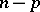 , then
, then 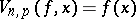 . A de la Vallée-Poussin sum may be written as follows
. A de la Vallée-Poussin sum may be written as follows
where the expressions
are said to be the de la Vallée-Poussin kernels.
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur la meilleure approximation des fonctions d'une variable réelle par des expressions d'ordre donné" C.R. Acad. Sci. Paris Sér. I. Math. , 166 (1918) pp. 799–802 |
| [2] | Ch.J. de la Vallée-Poussin, "Leçons sur l'approximation des fonctions d'une variable réelle" , Gauthier-Villars (1919) |
| [3] | I.P. Natanson, "Constructive function theory" , 1 , F. Ungar (1964) (Translated from Russian) |
| [4] | P.P. Korovkin, "Linear operators and approximation theory" , Hindushtan Publ. Comp. (1960) (Translated from Russian) |
| [5] | S.M. Nikol'skii, "Sur certaines méthodes d'approximation au moyen de sommes trigonométriques" Izv. Akad. Nauk SSSR Ser. Mat. , 4 : 6 (1940) pp. 509–520 |
| [6] | S.B. Stechkin, "On de la Vallée-Poussin sums" Dokl. Akad. Nauk SSSR , 80 : 4 (1951) pp. 545–520 (In Russian) |
| [7] | A.D. Shcherbina, "On a summation method of series, conjugate to Fourier series" Mat. Sb. , 27 (69) : 2 (1950) pp. 157–170 (In Russian) |
| [8] | A.F. Timan, "Approximation properties of linear methods of summation of Fourier series" Izv. Akad. Nauk SSSR Ser. Mat. , 17 (1953) pp. 99–134 (In Russian) |
| [9] | A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) (Translated from Russian) |
| [10] | A.V. Efimov, "On approximation of periodic functions by de la Vallée-Poussin sums" Izv. Akad. Nauk SSSR Ser. Mat. , 23 : 5 (1959) pp. 737–770 (In Russian) |
| [11] | A.V. Efimov, "On approximation of periodic functions by de la Vallée-Poussin sums" Izv. Akad. Nauk SSSR Ser. Mat. , 24 : 3 (1960) pp. 431–468 (In Russian) |
| [12] | S.A. Telyakovskii, "Approximation of differentiable functions by de la Vallée-Poussin sums" Dokl. Akad. Nauk SSSR , 121 : 3 (1958) pp. 426–429 (In Russian) |
| [13] | S.A. Telyakovskii, "Approximation to functions differentiable in Weyl's sense by de la Vallée-Poussin sums" Soviet Math. Dokl. , 1 : 2 (1960) pp. 240–243 Dokl. Akad. Nauk SSSR , 131 : 2 (1960) pp. 259–262 |
The de la Vallée-Poussin kernels are also given by the following formula, which in a way most clearly reveals their structure:
Here the 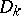 (
(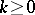 ) are the Dirichlet kernels (cf. Dirichlet kernel).
) are the Dirichlet kernels (cf. Dirichlet kernel).
How to Cite This Entry:
De la Vallée-Poussin sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_sum&oldid=12479
This article was adapted from an original article by A.V. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article

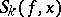 ,
, 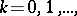 are the partial sums of the Fourier series of a function
are the partial sums of the Fourier series of a function 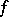 with period
with period 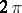 . If
. If 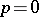 , the de la Vallée-Poussin sums become identical with the partial Fourier sums, and if
, the de la Vallée-Poussin sums become identical with the partial Fourier sums, and if  , they become identical with the Fejér sums (cf. Fejér sum). Ch.J. de la Vallée-Poussin [1], [2] was the first to study the method of approximating periodic functions by polynomials of the form (*); he also established the inequality
, they become identical with the Fejér sums (cf. Fejér sum). Ch.J. de la Vallée-Poussin [1], [2] was the first to study the method of approximating periodic functions by polynomials of the form (*); he also established the inequality
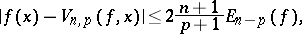
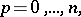
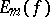 is the best uniform approximation of the function
is the best uniform approximation of the function 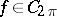 using trigonometric polynomials of order not greater than
using trigonometric polynomials of order not greater than 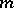 . If
. If 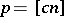 ,
, 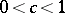 and
and 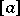 is the integer part of the number
is the integer part of the number  , the polynomials
, the polynomials 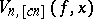 realize an approximation of order
realize an approximation of order 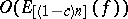 . The polynomials
. The polynomials 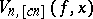 yield the best order approximations of continuous functions of period
yield the best order approximations of continuous functions of period 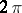 , with an estimate
, with an estimate 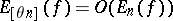 for certain values of
for certain values of 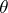 ,
, 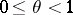 . The de la Vallée-Poussin sums have several properties which are of interest in the theory of summation of Fourier series. For instance, if
. The de la Vallée-Poussin sums have several properties which are of interest in the theory of summation of Fourier series. For instance, if 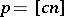 ,
, 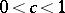 , then
, then 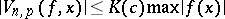 , and if
, and if 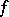 is a trigonometric polynomial of order not exceeding
is a trigonometric polynomial of order not exceeding 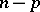 , then
, then 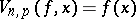 . A de la Vallée-Poussin sum may be written as follows
. A de la Vallée-Poussin sum may be written as follows
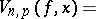
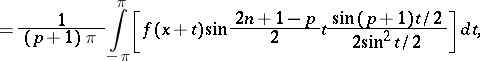
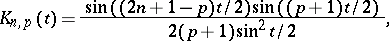

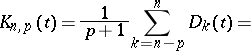
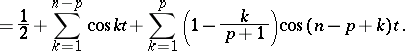
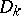 (
(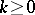 ) are the Dirichlet kernels (cf. Dirichlet kernel).
) are the Dirichlet kernels (cf. Dirichlet kernel).