Daubechies wavelets

A wavelet is a function that yields a basis in by means of translations and dyadic dilations of itself, i.e.,

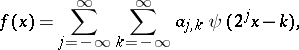for all (cf. also Wavelet analysis). Such a decomposition is called the discrete wavelet transform.

In 1988, the Belgian mathematician I. Daubechies constructed [a2] a class of wavelet functions , , that satisfy some special properties. First of all, the collection , , is an orthonormal system for fixed . Furthermore, each wavelet 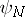is compactly supported (cf. also Function of compact support). Moreover, . The index number is also related to the number of vanishing moments, i.e.,

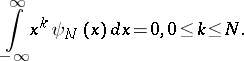A last important property of the Daubechies wavelets is that their regularity increases linearly with their support width. In fact,

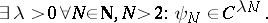For large 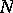one has .

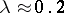The Daubechies wavelets are neither symmetric nor anti-symmetric around any axis, except for 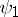, which is in fact the Haar wavelet [a3]. Satisfying symmetry conditions cannot go together with all other properties of the Daubechies wavelets.

The Daubechies wavelets can also be used for the continuous wavelet transform, i.e.

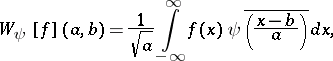for 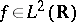, 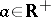and . The parameters and 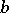denote scale and translation/position of the transform. A stable reconstruction formula exists for the continuous wavelet transform if and only if the following admissibility condition holds:

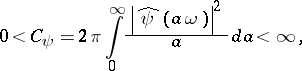where denotes the Fourier transform of 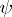. The reconstruction formula reads:

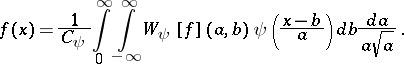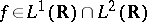This result holds weakly in . For and 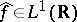, this results also holds pointwise.

All Daubechies wavelets satisfy the admissibility condition and thus guarantee a stable reconstruction.

References

[a1]	I. Daubechies, "Ten lectures on wavelets" , SIAM (1992)
[a2]	I. Daubechies, "Orthonormal bases of compactly supported wavelets" Commun. Pure Appl. Math. , 41 (1988) pp. 909–996
[a3]	A. Haar, "Zur theorie der orthogonalen Funktionensysteme" Math. Ann. , 69 (1910) pp. 331–371