Darboux vector
The vector 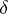 of the instantaneous axis of rotation around which the natural trihedral of a curve
of the instantaneous axis of rotation around which the natural trihedral of a curve 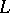 is rotating during the uniform movement of a point
is rotating during the uniform movement of a point  along the curve
along the curve 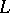 . The Darboux vector lies in the rectifying plane of the curve
. The Darboux vector lies in the rectifying plane of the curve 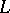 and is expressed in terms of the principal normal
and is expressed in terms of the principal normal 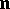 and the tangent
and the tangent 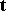 of
of 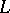 by the formula
by the formula
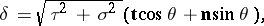 |
where  and
and 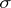 are the curvature and the torsion of
are the curvature and the torsion of 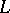 and
and 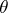 is the angle between the Darboux vector and the tangent to
is the angle between the Darboux vector and the tangent to 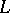 . The Frénet formulas may be written with the aid of the Darboux vector as follows:
. The Frénet formulas may be written with the aid of the Darboux vector as follows:
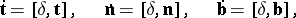 |
where 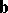 is the binormal of
is the binormal of 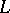 .
.
G. Darboux [1] was the first to point out the geometric significance of the Darboux vector for the natural trihedral of a space curve.
References
| [1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887) pp. 1–18 |
| [2] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 1 , Moscow-Leningrad (1947) (In Russian) |
Comments
The natural trihedral (a name used by S. Sternberg [a1]) is commonly called Frénet frame (also Frénet trihedron).
References
| [a1] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [a2] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
Darboux vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_vector&oldid=14668