Darboux surfaces
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
wreath of
Surfaces associated with an infinitesimal deformation of one of them; discovered by G. Darboux [1]. Darboux surfaces form a "wreath" of 12 surfaces, with radius vectors 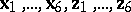 satisfying the equations
satisfying the equations
 |
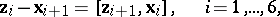 |
 |
where 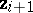 and
and 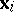 are in Peterson correspondence,
are in Peterson correspondence, 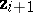 and
and 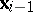 are in polar correspondence, while
are in polar correspondence, while 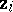 and
and  are poles of a
are poles of a 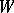 -congruence. A similar "wreath" is formed by pairs of isometric surfaces of an elliptic space.
-congruence. A similar "wreath" is formed by pairs of isometric surfaces of an elliptic space.
References
| [1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 4 , Gauthier-Villars (1896) |
| [2] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
Comments
For the notion of a 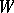 -congruence cf. Congruence of lines.
-congruence cf. Congruence of lines.
References
| [a1] | G. Fubini, E. Čech, "Introduction á la géométrie projective différentielle des surfaces" , Gauthier-Villars (1931) |
| [a2] | G. Bol, "Projective Differentialgeometrie" , Vandenhoeck & Ruprecht (1954) |
How to Cite This Entry:
Darboux surfaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_surfaces&oldid=18810
Darboux surfaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_surfaces&oldid=18810
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article