Darboux quadric

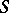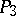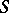A second-order surface with second-order contact with a surface in three-dimensional projective space at a point , in which the line of intersection with the surface at the point has a special type of singularity. Out of the set of quadrics with second-order contact with 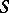at one can select the quadrics in which the line of intersection with 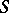has a singular point with three coincident tangents. On the surface 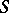there are three directions (Darboux directions) for these three coincident tangents. At 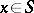there exists a one-parameter family of Darboux quadrics — the Darboux pencil. 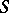A pencil of hyper-quadrics, which are in contact at a point with a hypersurface in projective space 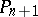, is an extension of the Darboux pencil. A (non-developable) hypersurface 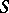degenerates into a hyper-quadric if and only if its generalized Darboux tensor vanishes [2].

References

[1]	S.P. Finikov, "Projective-differential geometry" , Moscow-Leningrad (1937) (In Russian)
[2]	G.F. Laptev, "Differential geometry of imbedded manifolds. Group theoretical methods of differential geometric investigation" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–382 (In Russian)

References

[a1]	E. Cartan, "Leçons sur la théorie des espaces à connexion projective" , Gauthier-Villars (1937) pp. Part II, Chapt. VI §II