Darboux equation

An ordinary differential equation

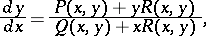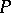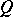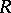where , and are integral polynomials in and 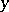. This equation was first studied by G. Darboux [1]. The Jacobi equation is a special case of the Darboux equation. Let be a highest degree of the polynomials 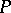, , 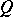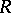; if the Darboux equation has known particular algebraic solutions, then if 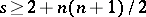, its general solution is found without quadratures, and if 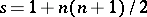, an integrating factor can be found [2]. If and are homogeneous functions of degree , and 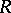is a homogeneous function of degree 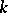then, if 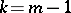, the Darboux equation is a homogeneous differential equation; if 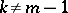, the Darboux equation may be reduced to a Bernoulli equation by substituting .

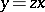References

[1]	G. Darboux, "Mémoire sur les équations différentielles algébriques du premier ordre et du premier degré" Bull. Sci. Math. , 2 (1878) pp. 60–96
[2]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)

N.Kh. Rozov

The hyperbolic equation

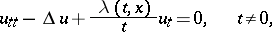where 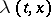is a non-negative continuously-differentiable function of 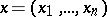. The following uniqueness theorem is valid both for the solution of the Darboux equation and for the solution of the wave equation. If some twice continuously-differentiable solution 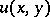of the Darboux equation vanishes together with its derivative on the base of the characteristic cone lying in the plane 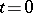, it vanishes inside the entire domain bounded by this cone. The form of the characteristic cone is the same as for the wave equation. If 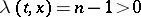, the solution of the Darboux equation satisfying the initial conditions

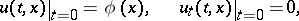with a twice continuously-differentiable function 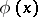, is the function

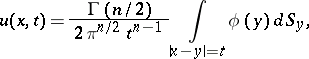where 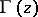is the gamma-function. This solution of the Darboux equation and the solution 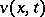of the wave equation satisfying the conditions

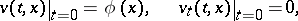are connected by the relation

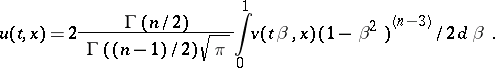The equation was named after G. Darboux.

References

[1]	F. John, "Plane waves and spherical means applied to partial differential equations" , Interscience (1955)