Darboux-Baire-1-function
Darboux–Baire one-function, Darboux function of the first Baire class
A real-valued function of a real variable of the first Baire class (cf. Baire classes) that satisfies the Darboux property.
In the first Baire class, the Darboux property is known to be equivalent to other properties. For example, in 1907, J. Young considered [a19] the following property: For each 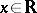 there exist sequences
there exist sequences 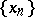 ,
, 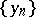 such that
such that  and
and
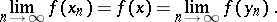 |
He proved that for functions of the first Baire class, the Darboux property and this Young property are equivalent. In 1922, K. Kuratowski and W. Sierpiński proved [a10] that for real-valued functions of the first Baire class and defined on an interval, the Darboux property is equivalent to the fact that the function has a connected graph (cf. also Graph of a mapping). In 1974, J. Brown showed [a3] that for real functions of the first Baire class and defined on an interval, the Darboux property is equivalent to Stallings almost continuity. In 1988, it was shown [a4] that for a function 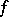 of the first Baire class, the Darboux property of
of the first Baire class, the Darboux property of 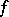 is equivalent to extendibility of
is equivalent to extendibility of 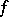 . In 1995, it was proved [a7] that a function
. In 1995, it was proved [a7] that a function 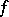 in the first Baire class is a Darboux function if and only if
in the first Baire class is a Darboux function if and only if 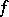 is first return continuous.
is first return continuous.
The set of all Darboux functions 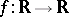 of the first Baire class will be denoted by
of the first Baire class will be denoted by 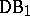 . The class
. The class 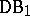 contains many important classes of functions, for example the class
contains many important classes of functions, for example the class 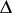 of all (finite) derivatives, the class
of all (finite) derivatives, the class 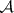 of all Stallings almost-continuous functions, and the class
of all Stallings almost-continuous functions, and the class 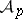 of all approximately continuous functions (cf. also Approximate continuity). For bounded functions (denoted by the prefix
of all approximately continuous functions (cf. also Approximate continuity). For bounded functions (denoted by the prefix 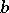 ),
),
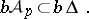 |
One can prove [a5] that in 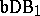 (with the metric of the uniform convergence) the sets
(with the metric of the uniform convergence) the sets 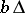 and
and 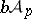 are very small, in fact, they are superporous at each point of
are very small, in fact, they are superporous at each point of 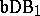 . I. Maximoff proved ([a12], [a13], [a11]) that each function from the larger class (
. I. Maximoff proved ([a12], [a13], [a11]) that each function from the larger class (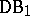 ) can be transformed into a function from the smaller class
) can be transformed into a function from the smaller class  (or
(or 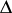 ) by a suitable homeomorphic change of variables. In 1961, C. Goffman and D. Waterman considered [a9] connections between
) by a suitable homeomorphic change of variables. In 1961, C. Goffman and D. Waterman considered [a9] connections between 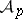 and
and 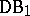 for functions mapping a Euclidean space into a metric space.
for functions mapping a Euclidean space into a metric space.
In 1950, Z. Zahorski considered [a20] the following hierarchy of classes of functions:
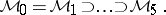 |
Each of these classes is defined in terms of an associated set of a function (the associated sets of 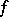 are all sets of the form
are all sets of the form 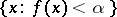 and
and 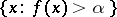 ). The two largest classes
). The two largest classes 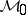 and
and  are equal to
are equal to 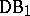 , the smallest class (
, the smallest class ( ) is equal to
) is equal to 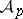 . Zahorski also proved that the class
. Zahorski also proved that the class 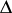 fits into this "sequence of classes of functions" (if
fits into this "sequence of classes of functions" (if 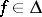 , then
, then 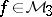 and if
and if 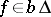 ; then
; then 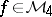 ). The similar hierarchy of classes of functions of two variables has been considered in [a14], [a15], [a18].
). The similar hierarchy of classes of functions of two variables has been considered in [a14], [a15], [a18].
The class 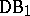 is closed with respect to uniform convergence. The maximal additive family for
is closed with respect to uniform convergence. The maximal additive family for 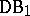 is the class of all continuous functions. The maximal multiplicative family for
is the class of all continuous functions. The maximal multiplicative family for 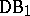 is the class of Darboux functions
is the class of Darboux functions 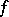 with the property: If
with the property: If 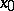 is a right-hand (left-hand) discontinuity point of
is a right-hand (left-hand) discontinuity point of 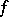 , then
, then 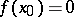 and there is a sequence
and there is a sequence 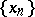 such that
such that 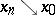 (respectively,
(respectively, 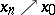 ) and
) and 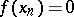 , [a8]. Of course,
, [a8]. Of course, 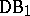 does not form a ring, but for each function
does not form a ring, but for each function 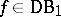 there exists a ring
there exists a ring 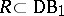 containing the class of all continuous functions and
containing the class of all continuous functions and 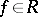 (see, e.g., [a18]).
(see, e.g., [a18]).
In 1963, H. Croft constructed [a6] a function 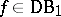 that is zero almost-everywhere but not identically zero. In 1974, a general method for constructing such functions was given ([a1], [a2]): Let
that is zero almost-everywhere but not identically zero. In 1974, a general method for constructing such functions was given ([a1], [a2]): Let 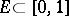 be an
be an 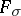 -set (cf. also Set of type
-set (cf. also Set of type 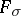 (
(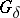 )) that is bilaterally c-dense-in-itself. Then there exists a function
)) that is bilaterally c-dense-in-itself. Then there exists a function  such that
such that 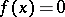 for
for 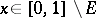 and
and 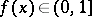 for all
for all 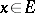 .
.
Except the standard class 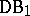 , one can also consider the class
, one can also consider the class 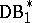 (
( if
if 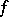 is a Darboux function and for every non-empty closed set
is a Darboux function and for every non-empty closed set 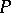 there is an open interval
there is an open interval 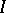 such that
such that 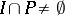 and
and 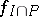 is continuous; see, e.g., [a17]).
is continuous; see, e.g., [a17]).
References
| [a1] | S. Agronsky, "Characterizations of certain subclasses of the Baire class 1" Doctoral Diss. Univ. Calif. Santa Barbara (1974) |
| [a2] | A.M. Bruckner, "Differentiation of real functions" , Springer (1978) |
| [a3] | J.B. Brown, "Almost continuous Darboux functions and Reed's pointwise convergence criteria" Fund. Math. , 86 (1974) pp. 1–7 |
| [a4] | J.B. Brown, P.L. Humke, "Measurable Darboux functions" Proc. Amer. Math. Soc. , 102 : 3 (1988) pp. 603–610 |
| [a5] | B. Świątek, "The functions spaces 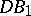 and and 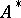 " Doctoral Diss. Univ. Lódź (1997) " Doctoral Diss. Univ. Lódź (1997) |
| [a6] | H. Croft, "A note on a Derboux continuous function" J. London Math. Soc. , 38 (1963) pp. 9–10 |
| [a7] | U.B. Darji, M.J. Evans, R.J. O'Malley, "First return path systems: differentiability, continuity and orderings" Acta Math. Hung. , 66 (1995) pp. 83–103 |
| [a8] | R. Fleissner, "A note on Baire 1 Darboux functions" Real Anal. Exch. , 3 (1977-78) |
| [a9] | C. Goffman, D. Waterman, "Approximately continuous transformations" Proc. Amer. Math. Soc. , 12 (1916) pp. 116–121 |
| [a10] | K. Kuratowski, W. Sierpiński, "Les fonctions de classe 1 et les ensembles convecs punctiformes" Fund. Math. , 3 (1922) pp. 303–313 |
| [a11] | I. Maximoff, "On continuous transformation of some functions into an ordinary derivative" Ann. Scuola Norm. Sup. Pisa , 12 (1943) pp. 147–160 |
| [a12] | I. Maximoff, "Sur la transformation continue de fonctions" Bull. Soc. Phys. Math. Kazan. , 3 : 12 (1940) pp. 9–41 (In Russian) (French summary) |
| [a13] | I. Maximoff, "Sur la transformation continue de quelques fonctions en dérivées exactes" Bull. Soc. Phys. Math. Kazan. , 3 : 12 (1940) pp. 57–81 (In Russian) (French summary) |
| [a14] | L. Mišik, "Über die Eigenschaft von Darboux und einiger Klassen von Funktionen" Rev. Roum. Math. Pures Appl. , 11 (1966) pp. 411–430 |
| [a15] | L. Mišik, "Über die Klasse 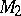 " Časop. Pro Pěst. Mat. , 91 (1966) pp. 389–411 " Časop. Pro Pěst. Mat. , 91 (1966) pp. 389–411 |
| [a16] | T. Natkaniec, "Almost continuity" Habilitation Thesis Bydgoszcz (1992) |
| [a17] | R.J. O'Malley, "Baire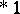 , Darboux functions" Proc. Amer. Math. Soc. , 60 (1976) pp. 187–192 , Darboux functions" Proc. Amer. Math. Soc. , 60 (1976) pp. 187–192 |
| [a18] | R.J. Pawlak, "Darboux transformations" Habilitation Thesis Univ. Lodz (1985) (In Polish) |
| [a19] | J. Young, "A theorem in the theory of functions of a real variable" Rend. Circ. Mat. Palermo , 24 (1907) pp. 187–192 |
| [a20] | Z. Zahorski, "Sur la prémiere dérivée" Trans. Amer. Math. Soc. , 69 (1950) pp. 1–54 |
Darboux-Baire-1-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux-Baire-1-function&oldid=18540