D'Alembert operator
From Encyclopedia of Mathematics
wave operator, d'Alembertian
The second-order differential operator which in Cartesian coordinates assumes the following form:
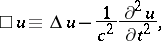 |
where  is the Laplace operator and
is the Laplace operator and  is a constant. Its form in spherical coordinates is:
is a constant. Its form in spherical coordinates is:
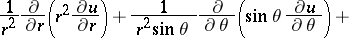 |
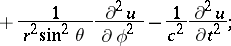 |
in cylindrical coordinates:
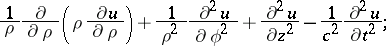 |
in general curvilinear coordinates:
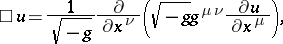 |
where  is the determinant of the matrix
is the determinant of the matrix  formed from the coefficients of the metric tensor
formed from the coefficients of the metric tensor  .
.
Named after J. d'Alembert (1747), who considered its simplest form when solving the one-dimensional wave equation.
Comments
In the last equation above, the Einstein (summation) convention applies to the right-hand side (i.e. there is a summation involved over all 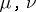 ).
).
References
| [a1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [a2] | F. John, "Partial differential equations" , Springer (1968) |
How to Cite This Entry:
D'Alembert operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=D%27Alembert_operator&oldid=11498
D'Alembert operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=D%27Alembert_operator&oldid=11498
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article