D'Alembert criterion (convergence of series)
From Encyclopedia of Mathematics
If for a series of numbers,
 |
there exists a number 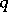 ,
,  , such that, from a certain term onwards, the inequality
, such that, from a certain term onwards, the inequality
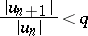 |
is satisfied, the series converges absolutely; if, from a certain term onwards,
 |
the series diverges. In particular, if the limit
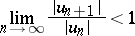 |
exists, the series converges absolutely, and if
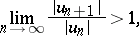 |
it diverges. For example, the series
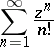 |
converges absolutely for all complex  , since
, since
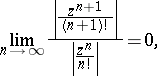 |
while the series 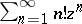 diverges for all
diverges for all 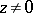 since
since
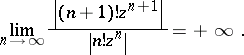 |
If
 |
the series may converge or diverge; this condition is satisfied by the two series
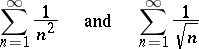 |
the first series being convergent, while the second is divergent.
Established by J. d'Alembert (1768).
Comments
This criterion also goes by the name of ratio test, cf. [a1].
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
How to Cite This Entry:
D'Alembert criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=D%27Alembert_criterion_(convergence_of_series)&oldid=14634
D'Alembert criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=D%27Alembert_criterion_(convergence_of_series)&oldid=14634
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article