Cylindrical surface (cylinder)
The surface formed by the motion of a line (the generator) moving parallel to itself and intersecting a given curve (the directrix).
The directrix of a cylindrical surface of the second order is a curve of the second order. Depending on the form of the directrix one distinguishes an elliptic cylinder, the canonical equation of which is
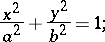 |
an imaginary elliptic cylinder:
 |
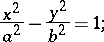 |
and a parabolic cylinder:
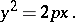 |
If the directrix is a degenerate curve of the second order (i.e. a pair of lines), then the cylindrical surface is a pair of planes (intersecting, parallel or coincident, real or imaginary, depending on the corresponding property of the directrix).
A cylindrical surface of order  is an algebraic surface given in some affine coordinate system
is an algebraic surface given in some affine coordinate system  by an algebraic equation of degree
by an algebraic equation of degree  not containing one of the coordinates (for example,
not containing one of the coordinates (for example,  ):
):
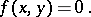 | (*) |
The curve of order  defined by equation (*) is sometimes called the base of the cylindrical surface.
defined by equation (*) is sometimes called the base of the cylindrical surface.
Cylindrical surface (cylinder). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cylindrical_surface_(cylinder)&oldid=15188