Cyclotomic field
A field  obtained from the field
obtained from the field  of rational numbers by adjoining a primitive
of rational numbers by adjoining a primitive  -th root of unity
-th root of unity  , where
, where  is a natural number. The term (local) cyclotomic field is also sometimes applied to the fields
is a natural number. The term (local) cyclotomic field is also sometimes applied to the fields  , where
, where  is the field of rational
is the field of rational  -adic numbers. Since
-adic numbers. Since  when
when  is odd, it is usually assumed that
is odd, it is usually assumed that 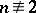 (
(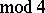 ). Distinct
). Distinct  then correspond to non-isomorphic fields
then correspond to non-isomorphic fields 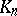 .
.
Cyclotomic fields arise naturally in the cyclotomy problem — the division of a circle into  equal parts is equivalent to the construction of a primitive root
equal parts is equivalent to the construction of a primitive root 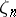 in the complex plane. The structure of cyclotomic fields is "fairly simple" , and they therefore provide convenient experimental material in formulating general concepts in number theory. For example, the concept of an algebraic integer and a divisor first arose in the study of cyclotomic fields.
in the complex plane. The structure of cyclotomic fields is "fairly simple" , and they therefore provide convenient experimental material in formulating general concepts in number theory. For example, the concept of an algebraic integer and a divisor first arose in the study of cyclotomic fields.
The special position of cyclotomic fields among all algebraic number fields is illustrated by the Kronecker–Weber theorem, which states that a finite extension  is Abelian if and only if
is Abelian if and only if 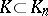 for some
for some  . An analogous proposition holds for local cyclotomic fields.
. An analogous proposition holds for local cyclotomic fields.
Algebraic theory.
The field 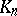 is an Abelian extension of
is an Abelian extension of  with Galois group
with Galois group
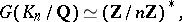 |
where 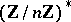 is the multiplicative group of the ring of residues modulo
is the multiplicative group of the ring of residues modulo  . In particular, the degree
. In particular, the degree 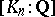 is
is  , where
, where 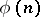 is Euler's function. The field
is Euler's function. The field 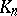 is totally imaginary and of degree 2 over its maximal totally real subfield
is totally imaginary and of degree 2 over its maximal totally real subfield  .
.
If  is the factorization of
is the factorization of  into prime numbers, then
into prime numbers, then 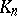 is the linearly disjoint compositum of the fields
is the linearly disjoint compositum of the fields 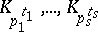 . In the field
. In the field 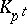 the prime divisor
the prime divisor  has ramification index
has ramification index  . In the same field one has the following equality of principal divisors:
. In the same field one has the following equality of principal divisors: 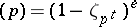 . All other prime divisors of
. All other prime divisors of 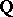 are unramified in
are unramified in 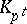 , whence it follows that
, whence it follows that 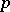 is ramified in
is ramified in  if and only if
if and only if 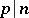 .
.
The numbers  form an integral basis for the field
form an integral basis for the field 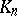 . The discriminant of
. The discriminant of 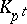 is equal to
is equal to 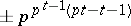 . If
. If 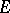 and
and 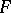 are fields which are linearly disjoint over
are fields which are linearly disjoint over 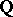 with relatively prime discriminants
with relatively prime discriminants  and
and 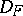 , then
, then 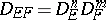 , where
, where 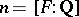 ,
, 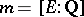 . This makes it possible to calculate
. This makes it possible to calculate 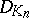 for arbitrary
for arbitrary  (see [3]).
(see [3]).
For the field 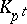 , the numbers
, the numbers
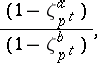 |
where 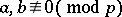 , generate a subgroup of finite index in the group of all units. The elements of this subgroup are known as circular units or cyclotomic units.
, generate a subgroup of finite index in the group of all units. The elements of this subgroup are known as circular units or cyclotomic units.
The decomposition law for cyclotomic fields, that is, the law according to which the prime divisors 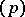 in
in 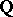 factorize into prime divisors in
factorize into prime divisors in 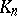 , is a particular case of the general decomposition law in Abelian extensions, established in class field theory (see [4]). Explicitly: If
, is a particular case of the general decomposition law in Abelian extensions, established in class field theory (see [4]). Explicitly: If  and if
and if  is the least natural number such that
is the least natural number such that 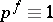 (
(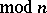 ), then in
), then in 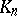 ,
,
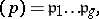 |
where the prime divisors  are pairwise distinct,
are pairwise distinct, 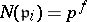 and
and 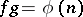 . Thus, the factorization type of
. Thus, the factorization type of 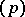 depends only on the residue of
depends only on the residue of 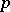 (
(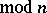 ). If
). If 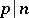 , the exact form of the factorization of
, the exact form of the factorization of  can be obtained, using the facts that
can be obtained, using the facts that  , where
, where  and
and 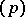 is totally ramified in
is totally ramified in 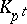 .
.
If 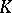 is the maximal Abelian extension of
is the maximal Abelian extension of 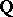 , then
, then 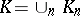 and
and
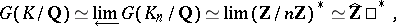 |
where 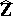 is the completion of the ring of integers
is the completion of the ring of integers  with respect to all ideals of finite index. In particular, for any prime number
with respect to all ideals of finite index. In particular, for any prime number 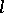 there is a unique extension
there is a unique extension 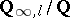 with Galois group isomorphic to the group of
with Galois group isomorphic to the group of 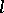 -adic integers
-adic integers  .
.
According to class field theory, there exists a reciprocity map
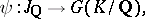 |
where 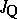 is the idèle group of
is the idèle group of 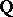 . In the case of a cyclotomic field
. In the case of a cyclotomic field 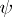 admits a simple explicit description (see [4]).
admits a simple explicit description (see [4]).
Analytic theory.
Many results regarding the structure of the divisor class group of 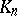 can be proved by analytic methods. If
can be proved by analytic methods. If 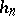 is the class number of
is the class number of  , then
, then
 |
here  and
and  are, respectively, the number of roots of unity, the discriminant and the regulator of
are, respectively, the number of roots of unity, the discriminant and the regulator of  ,
, 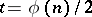 , and
, and 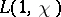 is the Dirichlet
is the Dirichlet  -function for the character
-function for the character 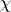 , where
, where 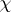 runs through all non-trivial primitive multiplicative characters modulo
runs through all non-trivial primitive multiplicative characters modulo  . The function
. The function 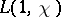 in turn can be expressed explicitly in terms of Gauss sums (see [7]). This solves the problem of calculating
in turn can be expressed explicitly in terms of Gauss sums (see [7]). This solves the problem of calculating 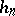 , given
, given  .
.
There is a natural decomposition of 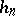 into two factors,
into two factors, 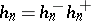 ; the first and second factor of the class number, where
; the first and second factor of the class number, where 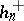 is interpreted as the class number of the field
is interpreted as the class number of the field 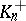 . If
. If 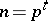 then
then 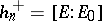 , where
, where 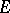 is the group of units of
is the group of units of 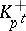 and
and 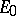 is the group of real cyclotomic units (any cyclotomic unit becomes real if multiplied by a suitable root of unity).
is the group of real cyclotomic units (any cyclotomic unit becomes real if multiplied by a suitable root of unity).
In questions related to the Fermat problem, an important role is played by the divisibility of the class number of 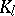 by
by 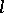 , where
, where 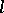 is prime. It is known that
is prime. It is known that 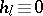 (
(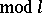 ) for infinitely many prime numbers
) for infinitely many prime numbers 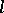 (such numbers
(such numbers 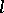 are said to be irregular). As to the set of regular prime numbers
are said to be irregular). As to the set of regular prime numbers 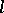 , i.e. numbers for which
, i.e. numbers for which 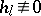 (
(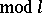 ), it is not known (1982) whether it is finite or infinite. It has been conjectured that
), it is not known (1982) whether it is finite or infinite. It has been conjectured that 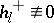 (
(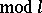 ) for all
) for all 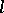 , and this has been confirmed in a large number of cases. The factor
, and this has been confirmed in a large number of cases. The factor 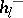 is more amenable to investigation. There exists a relatively simple criterion for the divisibility of
is more amenable to investigation. There exists a relatively simple criterion for the divisibility of 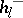 (and
(and 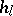 ) by
) by 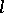 in terms of Bernoulli numbers ([7]). It is known that
in terms of Bernoulli numbers ([7]). It is known that 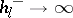 as
as 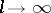 and that
and that 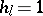 if and only if
if and only if 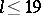 (see [6]).
(see [6]).
The so-called 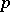 -adic
-adic 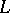 -functions have been successfully applied to the study of the class groups of cyclotomic fields (see [5], [8]).
-functions have been successfully applied to the study of the class groups of cyclotomic fields (see [5], [8]).
References
| [1] | E. Kummer, "Ueber die Zerlegung der aus Wurzeln der Einheit gebildeten komplexen Zahlen in ihre Primfaktoren" J. Reine Angew. Math. , 35 (1847) pp. 327–367 |
| [2] | H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) |
| [3] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) |
| [4] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) |
| [5] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [6] | K. Uchida, "Class numbers of imaginary abelian number fields III" Tôhoku Math. J. , 23 (1971) pp. 573–580 |
| [7] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1975) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [8] | K. Iwasawa, "Lectures on 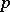 -adic -adic 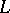 -functions" , Springer (1972) -functions" , Springer (1972) |
| [9] | S. Lang, "Cyclotomic fields" , Springer (1978) |
Comments
It is still not known whether there are infinitely many regular primes (1987), but it is conjectured that the density of the set of regular primes inside the set of all primes is  , see [a5]. It has been proved (for
, see [a5]. It has been proved (for 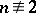
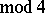 ) that
) that 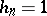 if and only if
if and only if 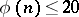 or
or 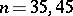 or
or 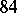 , see [a3], [a5]. An important theorem that describes the structure of the class groups of cyclotomic fields in terms of
, see [a3], [a5]. An important theorem that describes the structure of the class groups of cyclotomic fields in terms of 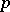 -adic
-adic 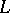 -functions has been proved by B. Mazur and A. Wiles (see [a1], [a4]) with the help of methods from algebraic geometry.
-functions has been proved by B. Mazur and A. Wiles (see [a1], [a4]) with the help of methods from algebraic geometry.
References
| [a1] | J. Coates, "The work of Mazur and Wiles on cyclotomic fields." Sem. Bourbaki , 33 : 575 (1980/81) Lecture Notes in Math. , 901 (1981) pp. 220–242 |
| [a2] | S. Lang, "Cyclotomic fields" , II , Springer (1980) |
| [a3] | J.M. Masley, H.L. Montgomery, "Cyclotomic fields with unique factorization" J. Reine Angew. Math. , 286–287 (1976) pp. 248–256 |
| [a4] | B. Mazur, A. Wiles, "Class fields of abelian extensions of 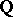 " Invent. Math. , 76 (1984) pp. 179–330 " Invent. Math. , 76 (1984) pp. 179–330 |
| [a5] | L.C. Washington, "Cyclotomic fields" , Springer (1982) |
Cyclotomic field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclotomic_field&oldid=17438