Cycloid
The plane transcendental curve that is the trajectory of a point of a circle rolling along a straight line (Fig. a).

Figure: c027540a
The parametric equations are:
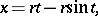 |
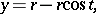 |
where  is the radius of the circle and
is the radius of the circle and  the angle of rotation of the circle. In Cartesian coordinates the equation is:
the angle of rotation of the circle. In Cartesian coordinates the equation is:
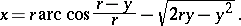 |
A cycloid is a periodic curve: the period (basis) is  . The points
. The points  ,
,  are cusps. The points
are cusps. The points  and
and  are the so-called vertices. The area is
are the so-called vertices. The area is  , the radius of curvature is
, the radius of curvature is 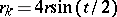 .
.
If the curve is described by a point lying outside (inside) a circle rolling along a line, then it is called an extended, (or elongated, Fig. b), a contracted, (or shortened, Fig. c) cycloid or sometimes a trochoid.

Figure: c027540b

Figure: c027540c
The parametric equations are
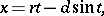 |
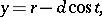 |
where  is the distance of the point
is the distance of the point  from the centre of the rolling circle.
from the centre of the rolling circle.
The cycloid is a tautochronic (or isochronic) curve, that is, a curve for which the time of descent of a material point along this curve from a certain height under the action of gravity does not depend on the original position of the point on the curve.
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
Cycloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cycloid&oldid=11749