Cyclic vector
Let  be an endomorphism of a finite-dimensional vector space
be an endomorphism of a finite-dimensional vector space  . A cyclic vector for
. A cyclic vector for  is a vector
is a vector  such that
such that  form a basis for
form a basis for  , i.e. such that the pair
, i.e. such that the pair  is completely reachable (see also Pole assignment problem; Majorization ordering; System of subvarieties; Frobenius matrix).
is completely reachable (see also Pole assignment problem; Majorization ordering; System of subvarieties; Frobenius matrix).
A vector  in an (infinite-dimensional) Banach space or Hilbert space with an operator
in an (infinite-dimensional) Banach space or Hilbert space with an operator  on it is said to be cyclic if the linear combinations of the vectors
on it is said to be cyclic if the linear combinations of the vectors 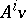 ,
, 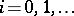 , form a dense subspace, [a1].
, form a dense subspace, [a1].
More generally, let 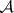 be a subalgebra of
be a subalgebra of 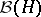 , the algebra of bounded operators on a Hilbert space
, the algebra of bounded operators on a Hilbert space 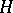 . Then
. Then 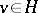 is cyclic if
is cyclic if 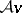 is dense in
is dense in 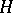 , [a2], [a5].
, [a2], [a5].
If 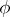 is a unitary representation of a (locally compact) group
is a unitary representation of a (locally compact) group 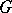 in
in  , then
, then  is called cyclic if the linear combinations of the
is called cyclic if the linear combinations of the  ,
, 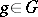 , form a dense set, [a3], [a4]. For the connection between positive-definite functions on
, form a dense set, [a3], [a4]. For the connection between positive-definite functions on  and the cyclic representations (i.e., representations that admit a cyclic vector), see Positive-definite function on a group. An irreducible representation is cyclic with respect to every non-zero vector.
and the cyclic representations (i.e., representations that admit a cyclic vector), see Positive-definite function on a group. An irreducible representation is cyclic with respect to every non-zero vector.
References
| [a1] | M. Reed, B. Simon, "Methods of mathematical physics: Functional analysis" , 1 , Acad. Press (1972) pp. 226ff |
| [a2] | R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1 , Acad. Press (1983) pp. 276 |
| [a3] | S.A. Gaal, "Linear analysis and representation theory" , Springer (1973) pp. 156 |
| [a4] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) pp. 53 (In Russian) |
| [a5] | M.A. Naimark, "Normed rings" , Noordhoff (1964) pp. 239 (In Russian) |
Cyclic vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclic_vector&oldid=18561