Cyclic group
From Encyclopedia of Mathematics
A group with a single generator. All cyclic groups are Abelian. Every finite group of prime order is cyclic. For every finite number  there is one and, up to isomorphism, only one cyclic group of order
there is one and, up to isomorphism, only one cyclic group of order  ; there is also one infinite cyclic group, which is isomorphic to the additive group
; there is also one infinite cyclic group, which is isomorphic to the additive group 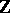 of integers. A finite cyclic group
of integers. A finite cyclic group 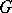 of order
of order  is isomorphic to the additive group of the ring of residues
is isomorphic to the additive group of the ring of residues 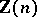 modulo
modulo  (and also to the group
(and also to the group 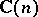 of (complex)
of (complex)  -th roots of unity). Every element
-th roots of unity). Every element  of order
of order  can be taken as a generator of this group. Then
can be taken as a generator of this group. Then
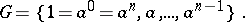 |
How to Cite This Entry:
Cyclic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclic_group&oldid=13750
Cyclic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclic_group&oldid=13750
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article