Cut
in a domain  along a non-closed simple arc
along a non-closed simple arc 
The removal of the points of the arc  from the domain
from the domain  , that is, replacing the domain
, that is, replacing the domain  by the domain (or domains)
by the domain (or domains)  , as well as the set
, as well as the set  itself. Here it is assumed that either the whole arc
itself. Here it is assumed that either the whole arc  or the whole arc except the initial or end point
or the whole arc except the initial or end point  belongs to
belongs to 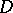 and that
and that 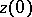 or
or 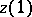 belong to the boundary
belong to the boundary 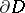 . To each point
. To each point 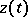 of the cut
of the cut  , when
, when 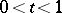 , there correspond two prime ends of the part of the domain
, there correspond two prime ends of the part of the domain 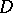 which belongs to
which belongs to 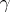 ; the left and right prime ends (cf. Limit elements). The union of these prime ends form the left and right-hand sides of the cut
; the left and right prime ends (cf. Limit elements). The union of these prime ends form the left and right-hand sides of the cut 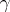 .
.
Comments
A cut is also called a slit.
One also speaks of boundary elements instead of limit elements or prime ends. These notions do not coincide in general, but for "nice" domains 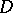 (e.g. with Jordan boundary) they can be identified. A related notion is that of a crosscut: an open simple arc that begins and ends at two different points of
(e.g. with Jordan boundary) they can be identified. A related notion is that of a crosscut: an open simple arc that begins and ends at two different points of 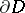 , cf. [a1], especially Chapt. 3.
, cf. [a1], especially Chapt. 3.
The word "cut" also occurs in several more meanings in various parts of mathematics. Thus, there is the notion of a Dedekind cut in the real or rational numbers, cf. Real number. The notion cut point on a geodesic line; and a cut or cutset in a graph or transportation network (cf. Flow in a network for the latter). Finally there are the cut locus and the cutting problem.
References
| [a1] | M. Ohtsuka, "Dirichlet problem, extremal length and prime ends" , v. Nostrand-Reinhold (1970) |
Cut. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cut&oldid=13864