Curvilinear integral
line integral
An integral along a curve. In  -dimensional Euclidean space
-dimensional Euclidean space 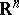 consider a given rectifiable curve
consider a given rectifiable curve 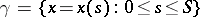 ,
, 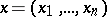 , where
, where  is the arc length; let
is the arc length; let 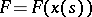 be a function defined on
be a function defined on 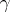 . The curvilinear integral
. The curvilinear integral
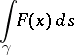 |
is defined by the equality
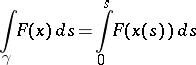 | (1) |
(the integral on the right is an integral over a real interval), and is called a line integral of the first kind, or a line integral with respect to arc length. It is the limit of suitable integral sums, which can be described in terms related to the curve. For example, if 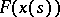 is Riemann-integrable (see Riemann integral),
is Riemann-integrable (see Riemann integral), 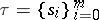 is a partition of
is a partition of 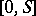 ,
, 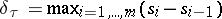 is its mesh,
is its mesh, 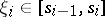 ,
, 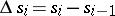 is the length of the section of
is the length of the section of 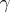 from the point
from the point 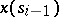 to the point
to the point 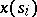 ,
, 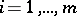 , and
, and
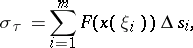 |
then
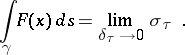 |
If the rectifiable curve 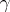 is given parametrically by
is given parametrically by 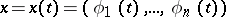 ,
, 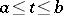 , and
, and 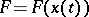 is a function defined on
is a function defined on 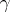 , then the integral
, then the integral
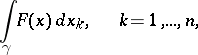 |
is defined by
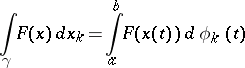 | (2) |
(the integral on the right is a Stieltjes integral), and is called a line integral of the second kind or a line integral with respect to the coordinate 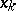 . It is also the limit of suitably constructed Riemann sums: If
. It is also the limit of suitably constructed Riemann sums: If 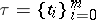 is a partition of
is a partition of 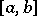 ,
, 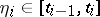 ,
, 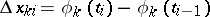 ,
, 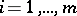 , and
, and
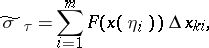 |
then
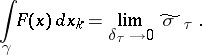 |
If 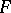 is a continuous function on
is a continuous function on 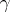 , then the curvilinear integrals (1) and (2) always exist. If
, then the curvilinear integrals (1) and (2) always exist. If 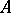 is the initial point and
is the initial point and 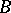 the end point of
the end point of 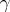 , then the curvilinear integrals (1) and (2) are denoted by
, then the curvilinear integrals (1) and (2) are denoted by
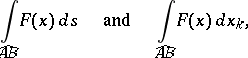 |
respectively.
Line integrals of the first kind are independent of the orientation of the curve:
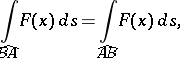 |
but line integrals of the second kind change sign when the orientation is reversed:
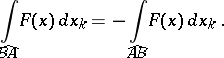 |
If 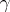 is a continuously differentiable curve given by a continuously differentiable representation
is a continuously differentiable curve given by a continuously differentiable representation 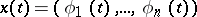 ,
, 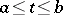 , and
, and 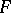 is a continuous function on
is a continuous function on 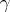 , then
, then
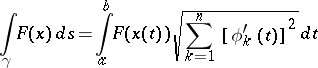 |
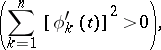 |
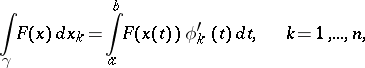 |
and hence the integrals on the right of these equalities are independent of the choice of the parameter on 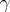 . If
. If 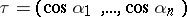 is a unit tangent vector to the curve
is a unit tangent vector to the curve 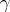 , then the line integral of the second kind may be expressed in terms of a line integral of the first kind via the formula
, then the line integral of the second kind may be expressed in terms of a line integral of the first kind via the formula
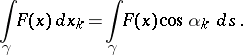 |
If 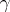 is given in vector notation
is given in vector notation 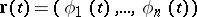 and
and 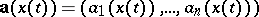 is a vector function defined on
is a vector function defined on 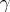 , then, by definition,
, then, by definition,
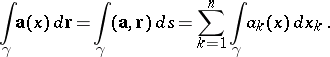 |
The relationship between line integrals and integrals of other types is established by the Green formulas and the Stokes formula.
Line integrals may be used to calculate the area of plane domains: If a finite plane domain 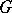 is bounded by a simple rectifiable curve
is bounded by a simple rectifiable curve 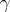 , then its area is
, then its area is
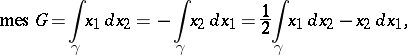 |
where the contour 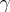 is oriented in the counter-clockwise sense.
is oriented in the counter-clockwise sense.
If 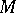 is a mass distributed over
is a mass distributed over 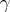 with linear density
with linear density 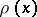 , then
, then
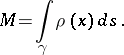 |
If 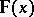 is the intensity of a force field (i.e. the force acting on a unit mass), then
is the intensity of a force field (i.e. the force acting on a unit mass), then
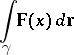 |
is equal to the work performed by the field in moving a unit mass along 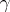 .
.
Line integrals are used in the theory of vector fields. If 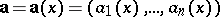 is a continuous vector field defined on some
is a continuous vector field defined on some  -dimensional domain
-dimensional domain 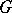 ,
, 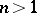 , then the following three properties are equivalent:
, then the following three properties are equivalent:
1) For any closed rectifiable curve 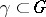 ,
,
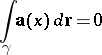 |
(a vector field possessing this property is called a potential field).
2) For any pair of points 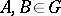 and any two rectifiable curves
and any two rectifiable curves 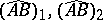 with initial point
with initial point 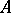 and end point
and end point 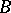 :
:
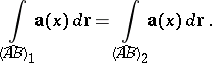 |
3) There exists in 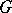 a function
a function 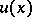 (called a potential function of the field
(called a potential function of the field 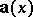 ), such that
), such that 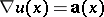 , i.e.
, i.e. 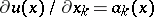 ,
, 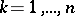 , and moreover, for any
, and moreover, for any 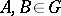 and any curve
and any curve 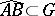 ,
,
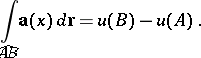 |
If 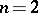 or
or  and
and 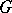 is a simply-connected domain (
is a simply-connected domain (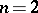 ) or a simply-connected surface (
) or a simply-connected surface (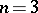 ), while the field
), while the field 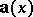 is continuously differentiable, then the properties 1)–3) are equivalent to the following property:
is continuously differentiable, then the properties 1)–3) are equivalent to the following property:
4) The rotation of the vector field vanishes in 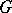 :
:
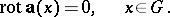 |
If 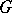 is not simply connected, then 4) need not be equivalent to 1)–3). For example, for the field
is not simply connected, then 4) need not be equivalent to 1)–3). For example, for the field
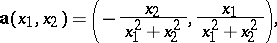 |
defined on the plane punctured at the origin one has 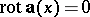 ,
, 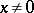 , but
, but
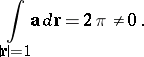 |
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "A course in mathematical analysis" , 2 , Moscow (1981) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian) |
Comments
Line integrals are a special instance of integrals of differential forms over chains, namely integrals of a 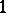 -form over a
-form over a 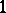 -chain (cf. Differential form; Chain and especially Integration on manifolds).
-chain (cf. Differential form; Chain and especially Integration on manifolds).
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 107–108 |
| [a2] | M. Spivak, "Calculus on manifolds" , Benjamin/Cummings (1965) |
Curvilinear integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvilinear_integral&oldid=15118