Curvature lines, net of
From Encyclopedia of Mathematics
An orthogonal net on a smooth hypersurface 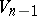 in an
in an  -dimensional Euclidean space
-dimensional Euclidean space 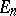 (
(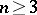 ), formed by the curvature lines (cf. Curvature line). A net of curvature lines on
), formed by the curvature lines (cf. Curvature line). A net of curvature lines on 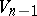 is a conjugate net. E.g., if
is a conjugate net. E.g., if 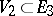 is a surface of revolution, the meridians and the parallels of latitude form a net of curvature lines. If
is a surface of revolution, the meridians and the parallels of latitude form a net of curvature lines. If 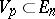 (
(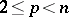 ) is a smooth
) is a smooth 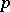 -dimensional surface with a field of one-dimensional normals such that the normal
-dimensional surface with a field of one-dimensional normals such that the normal 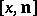 of the field lies in the second-order differential neighbourhood of the point
of the field lies in the second-order differential neighbourhood of the point  , then the normals of the field define curvature lines and a net of curvature lines on
, then the normals of the field define curvature lines and a net of curvature lines on 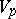 , exactly as on
, exactly as on 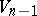 . However, a net of curvature lines on
. However, a net of curvature lines on 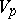 (
(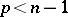 ) need not be conjugate.
) need not be conjugate.
References
| [1] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
| [2] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
Comments
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Curvature lines, net of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature_lines,_net_of&oldid=16117
Curvature lines, net of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature_lines,_net_of&oldid=16117
This article was adapted from an original article by V.T. Bazylev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article